System of Non-Linear Volterra Integral Equations in a Direct-Sum of Hilbert Spaces

Authors

  • Jabar Hassan Department of Mathematics, College of Science, Salahaddin University - Erbil / Iraq
  • Haider Majeed Department of Mathematics, Tikrit University, College of Education for Pure Sciences, Tikrit/ Iraq
  • Ghassan Ezzulddin Arif Department of Mathematics, Tikrit University, College of Education for Pure Sciences, Tikrit/ Iraq

Keywords:

system of non-linear integral equations, Reproducing kernel Hilbert spaces, Fixed point theorem

Abstract

We use the contraction mapping theorem to present the existence and uniqueness of solutions in a short time to a system of non-linear Volterra integral equations in a certain type of direct-sum H[a; b] of a Hilbert space V[a; b]. We extend the local existence and uniqueness of solutions to the global existence and uniqueness of solutions to the proposed problem. Because the kernel function is a transcendental function in H[a; b] on the interval [a; b], the results are novel and very important in numerical approximation.

Dimensions

K. A. Dawodu, “Extension of ADMM algorithm in solving optimal control model governed by partial di erential equation”, Journal of the Nigerian Society of Physical Sciences 3 (2021) 105. https://doi.org/10.46481/jnsps.2021.159.

V. O. Atabo & S. O. Adee, “A new special 15-step block method for solving general fourth order ordinary differential equations”, Journal of the Nigerian Society of Physical Sciences 3 (2021) 308. https://doi.org/10.46481/jnsps.2021.337.

M. I. Berenguer, D. Gamez, A. I. Garralda-Guillem, M. R. Galan & M. S. Perez, “Biorthogonal systems for solving Volterra integral equation systems of the second kind”, Journal of Computational and Applied Mathematics

(2011) 1875.

M. Cui & Y. Lin, “Nonlinear numerical analysis in reproducing kernel space”, Nova Science Publishers, Inc., 2009

L. Dai & R. N Jazar, Nonlinear approaches in engineering applications Springer, 2012.

J. S. Hassan & D. Grow, “New reproducing kernel hilbert spaces on semi-infinite domains with existence and uniqueness results for the nonhomogeneous telegraph equation. Mathematical Methods in the Applied Sciences 43 (2020) 9615.

J. S. Hassan & D. Grow, “Stability and approximation of solutions in new reproducing kernel hilbert spaces on a semi-infinite domain”, Mathematical Methods in the Applied Sciences 44 (2021) 12442

R. K Saeed & J. S Hassan, “Solving singular integral equations by using collocation method”, Mathematical Sciences Letters 3 (2014) 185.

L. H. Yang, J. H. Shen & Y. Wang, “The reproducing kernel method for solving the system of the linear volterra integral equations with variable coefficients”, Journal of Computational and Applied Mathematics 236 (2012) 2398.

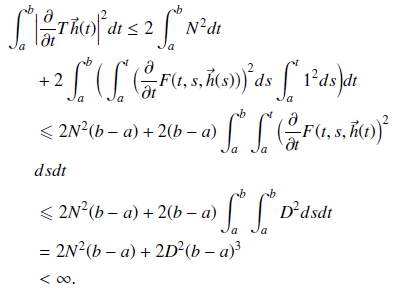
Published

2022-10-01

How to Cite

System of Non-Linear Volterra Integral Equations in a Direct-Sum of Hilbert Spaces. (2022). Journal of the Nigerian Society of Physical Sciences, 4(4), 1021. https://doi.org/10.46481/jnsps.2022.1021

Issue

Volume 4, Issue 4, November 2022

Section

Original Research
Copyright & Licensing

Copyright (c) 2022 Jabar Hassan, Haider, Ghassan

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

System of Non-Linear Volterra Integral Equations in a Direct-Sum of Hilbert Spaces. (2022). Journal of the Nigerian Society of Physical Sciences, 4(4), 1021. https://doi.org/10.46481/jnsps.2022.1021