Study of MHD SWCNT-Blood Nanofluid Flow in Presence of Viscous Dissipation and Radiation Effects through Porous Medium
Keywords:
SWCNT, Blood, Viscous dissipation, Radiation, Nusselt number, Skin frictionAbstract
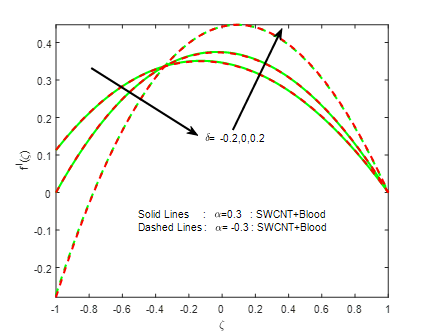
In this analysis, a computational study is conducted to examine the two-dimensional flow of an incompressible MHD SWCNT-blood nanofluid, saturated mass and porous medium .In addition to viscous dissipation, thermal radiation is taken into consideration. We developed the mathematical model and useful boundary intensity approximations to diminish the structure of partial differential equations based on the fluid for blood-based SWCNT underflow assumptions. Converted the partial differential equations by applying corresponding transformations to arrive at ODE’s. The above results are solved numerically by the Runge-Kutta 4th order technique. Noticed that there is desirable conformity when interpolated with the numerical one. The effects exhibited the velocity of SWCNT-blood nanofluid enhanced for defined standards of the viscosity parameter. Rise in temperature when various parameters like Prandtl number, Eckert number, and slip parameter are applied on SWCNT-blood. The impact of fluid flow on blood-based SWCNT is discussed graphically, and our results are tabulated along with illustrations. The design concepts, such as the Nusselt quantity and the local skin friction, conform to the analytical approach. Velocity reductions with an increase in CNT’s volume fraction, whereas enhancement in the blood temperature, is noted, which is directed to the rise in the heat mass transfer rates.
Published
How to Cite
Issue
Section
Copyright (c) 2023 M. Ramanuja, J. Kavitha, A. Sudhakar, N. Radhika

This work is licensed under a Creative Commons Attribution 4.0 International License.







