L-Stable Block Hybrid Numerical Algorithm for First-Order Ordinary Differential Equations

B. I. Akinnukawe; K. O. Muka

doi:10.46481/jnsps.2020.108

Authors

B. I. Akinnukawe
[email protected]
Department of Mathematics, University of Lagos, Lagos, Nigeria
K. O. Muka Department of Mathematics, University of Benin, Benin city, Nigeria

Keywords:

Second derivative, Stability, Hybrid, Block, Collocation techniques

Abstract

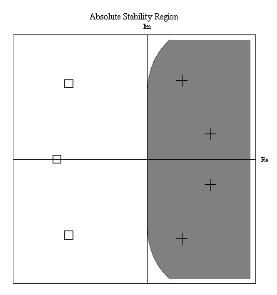
In this work, a one-step L-stable Block Hybrid Multistep Method (BHMM) of order five was developed. The method is constructed for solving first order Ordinary Differential Equations with given initial conditions. Interpolation and collocation techniques, with power series as a basis function, are employed for the derivation of the continuous form of the hybrid methods. The discrete scheme and its second derivative are derived by evaluating at the specific grid and off-grid points to form the main and additional methods respectively. Both hybrid methods generated are composed in matrix form and implemented as a block method. The stability and convergence properties of BHMM are discussed and presented. The numerical results of BHMM have proven its efficiency when compared to some existing methods.

Dimensions

REFERENCES

G. G. Dahlquist, “A special stability problem for linear multistep methods”, BIT 3 (1963) 27.

J. C. Butcher, The numerical methods for ordinary differential equations, John Wiley and Sons Ltd, Chichester, 2008.

J. D. Lambert, Computational methods for ordinary differential systems: The Initial Value Problems, Wiley, Chichester, 1973.

W. H. Enright, “Second derivative multistep methods for stiff ODEs”, SIAM Journal of Numerical Analysis 11 (1974) 321.

B. I. Akinnukawe & S. A. Okunuga, “A Seventh-order block integrator for solving stiff systems”, Nigerian Journal of Mathematics and Applications 24 (2015) 67.

C. W. Gear, “Hybrid methods for initial value problems in ordinary differential equations”, SIAM Journal of Numerical Analysis 2 (1965) 69.

S. A. Okunuga, “A fourth order composite two step method for stiff problems”, International Journal of Computer Mathematics 72 (1999) 39.

J. R. Cash, “On the integration of stiff systems of ODEs using Extended Backward Differentiation Formulae”, Numerische Mathematik 34 (1980) 235.

O. A. Akinfenwa, B. Akinnukawe & S. B. Mudasiru, “A family continuous third derivative block methods for solving stiff systems of first order ODEs”, Journal of the Nigerian Mathematical Society 34 (2015) 160.

O. A. Akinfenwa, S. A. Okunuga, B. I. Akinnukawe, U. P. Rufai & R. I. Abdulganiy, “Multi-derivative hybrid implicit Runge-Kutta method for solving stiff system of a first order differential equation”, Far East Journal of Mathematical Sciences (FJMS) 106 (2018) 543.

A. O. Adesanya, R. O. Onsachi & M. R. Odekunle, “New algorithm for first order stiff initial value problem”, Fasciculi Mathematici 58 (2017) 2.

A. P. Ijezie & K. O. Muka, “Modified SDBDF based on a non-zero root of the second characteristics polynomial”, Journal of Science and Technology Research 1 (2019) 128.

J. D. Lambert, Numerical methods for ordinary differential systems, John Wiley, New York, 1991.

P. Onumanyi, U. W. Sirisena & S. N. Jator. Continuous finite difference approximations for solving differential equations, “International Journal of Computational Mathematics”, 72 (1999) 15.

W. E. Milne, Numerical solution of differential equations, John Wiley, New York, 1953.

D. Sarafyan, Multistep methods for the numerical solution of ODEs made self-starting, Technical Report No. 495, Mathematics Research Center, Madison, Wisconsin, 1965.

L. F. Shampine & H. A.Watts, “Block implicit one-step methods”, Mathematics of Computation 23 (1969) 731.

S. O. Fatunla, “Block methods for second order IVPs”, Internal Journal of Computational Mathematics 41 (1991) 55.

P. Henrici, Discrete Variable Methods in ODEs, John Wiley, New York, 1962.

G. Hojjati, M. Y. Rahimi-Ardabili & S. M. Hosseini, “New second derivative multistep methods for stiff systems”, Applied Mathematical Modelling 30 (2006) 466.

G. A. Ismail & I. H. Ibrahim, “New efficient second derivative multistep methods for stiff systems”, Applied Mathematical Modelling 23 (1978) 279.

R. I. Okuonghae, M. N. O. Ikhile & J. Osemeke, “An off-step-point methods in multistep integration of stiff ODEs”, NMC Journal of Mathematical Sciences 3 (2014) 731.

A. K. Ezzeddine & G. Hojjati, “Third derivative multistep methods for stiff systems”, International Journal of Nonlinear Science 14 (2012) 443.