Analysis of an HIV - HCV simultaneous infection model with time delay

Authors

  • Adamu Shitu Hassan Department of Mathematical Sciences, Faculty of Physical Sciences, Bayero University, Kano, Nigeria
  • Nafiu Hussaini Department of Mathematical Sciences, Faculty of Physical Sciences, Bayero University, Kano, Nigeria

Keywords:

Delay, IV/HCV simultaneous infection, reproduction number, equilibrium, stability

Abstract

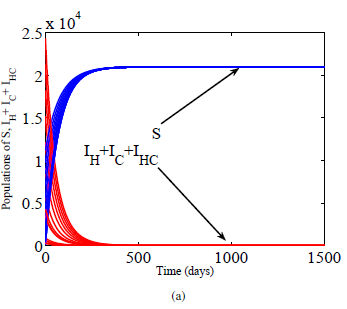
A novel mathematical delay model for simultaneous infection of HIV and hepatitis C virus is formulated and dynamically analyzed. Basic properties of the model are established and proved. Basic reproductive threshold is systematically calculated as the maximum of three subthreshold parameters. A disease free equilibrium is determined to be globally asymptotically stable for all values of the delay when the threshold is less than unity. However, when the threshold is greater than one, endemic equilibrium emerged which is shown to be locally asymptotically stable for any length of delay. Although the delay has no effect on stabilities of equilibria points, however, it is found to reduce the infectivity of the viruses as the length of the delay is increased. Epidemiological interpretations of the results and numerical simulations illustrating them are given.

Dimensions

World Health Organization: HIV and hepatitis coinfections. http://www.who.int. Accessed: November, 2018.

C. Castillo-Chavez, J. X. Velasco-Hernandez, “On the relationship between evolution of virulence and host demography”, Journal of Theoretical Biology, 192 (1998) 437.

S. Levin, D. Pimentel, “Selection of intermediate rates of increase in parasite-host systems”, The American Naturalist, 117 (1981) 308.

M. A. Nowak, R. M. May, “Superinfection and the evolution of parasite virulence”, Royal Society London series B, 255 (1994) 81.

S. Alizon, “Parasite co-transmission and the evolutionary epidemiology of virulence”, Evolution, 67 (2013) 921.

R. M. Anderson, R. M. May, Infectious Diseases of Humans Dynamics and Control, Oxford University Press, Oxford, UK 1991.

R. A. Frederick, C. B. Robert, “The dynamics of simultaneous infections with altered susceptibilities”, Theoretical Population Biology. 40 (1991) 369.

R. M. May, M. A. Nowak, “Coinfection and the evolution of parasite virulence”, Royal Society London, seies B, 261 (1995) 209.

Z. Mukandavire, A. B. Gumel, W. Garira, J. M. Tchuenche, “Mathematical analysis of a model for HIV-malaria co-infection”, Mathematical Bioscience and Engineering, 6 (2009) 333.

A. Y. C. Sanchez, M. Aerts, Z. Shkedy, P. Vickerman, F. Faggiano, “A mathematical model for HIV and Hepatitis C co-infection and its assessment from a statistical perspective”, Epidemics, 5 (2013) 56.

E. W. Seabloom, P. R. Hosseini, A. G. Power, E. T. Borer, “Diversity and Composition of Viral Communities: Coinfection of Barley and Cereal Yellow Dwarf Viruses in California Grasslands”, The American Naturalist, 173 (2009) 79.

M. van Baalen, M. W. Sabelis, “The dynamics of multiple infection and the evolution of virulence”, The American Naturalist, 146 (1995) 881.

A. Y. C. Sanchez, M. Aerts, Z. Shkedy, P. Vickerman, F. Faggiano, “A mathematical model for HIV and hepatitis C co-infection and its assessment from a statistical perspective”, Epidemics, 5 (2013) 56.

X-S. Zhang, K. F. Cao, “The impact of coinfections and their simultaneous transmission on antigenic diversity and epidemic cycling of infectious diseases”, Biomed Research Internatioal, (2014), 375 doi : 10:1155=2014=375862.

X-S. Zhang , A. De Angelis, P. J. White, A. Charlett, R. G. Pebody, J. McCauley, “Co-circulation of influenza A virus strains and emergence of pandemic via reassortment: the role of cross-immunity”, Epidemics, 5 (2013) 20.

O. Balmer, M. Tanner, “Prevalence and implications of multiple-strain infections”, Lancet Infectious Diseases, 11 (2011) 868.

R. Ridzon, K. Gallagher, C. Ciesielski, E. E. Mast, M. B. Ginsberg, B. J. Robertson, C. C. Luo, A. DeMaria, “Simultaneous transmission of human immunodeficiency virus and hepatitis C virus from a needle-stick injury”, The New England Journal of Medicine, 336 (1997) 919.

S. Gorman, N. L. Harvey, D. Moro, M. L. Lloyd, V. Voigt, L. M. Smith,

M. A. Lawson, G. R. Shellam, “Mixed infection with multiple strains of murine cytomegalovirus occurs following simultaneous or sequential infection of immunocompetent mice”, Journal of General Virology, 87 (2006) 1123.

G. Ippolito, V. Puro, N. Petrosillo, G. De Carli, G. Micheloni, E. Magliano, “Simultaneous infection with HIV and hepatitis C virus following occupational conjunctival blood exposure”, The Journal of the American Medical Association, 280 (1998), doi : 10:1001= jama:280:1:28:

W. Liu, Z. D. Li, F. Tang, M. Wei, Y. Tong, L. Zhang, Z. Xin, “Mixed infections of pandemic H1N1 and seasonal H3N2 viruses in outbreak”, Clinical Infectious Diseases, 50 (2010) 1359.

S. Telfer, X. Lambin, R. Birtles, P. Beldomenico, S. Burthe, S. Paterson, M. Begon, “Species interactions in a parasite community drive infection risk in a wildlife population”, Science 330 (2010) 243.

P. Schmid-Hempel, Evolutionary Parasitology: The Integrated Study of Infections, Immunology, Ecology and Genetics, Oxford University Press, Oxford, UK, 2011.

H. L. Smith, P. Waltman, The Theory of the Chemostat, Cambridge University Press, 1995.

X. Zhang, R. Pebody, D. De Angelis, P. J. White, A. Charlett, J. W. Mc- Cauley, “The possible impact of vaccination for seasonal influenza on emergence of pandemic influenza via reassortment”, PLoS ONE, 9 (2014) 12. doi : 10:1371= journal:pone:0114637.

A. Dutta, P. K. Gupta, “A mathematical model for transmission dynamics of HIV/AIDS with effect of weak CD4+ T cells”, Chinese Journal of Physics, 56 (2018) 1045.

W. Jia, J. Weng, C. Fang, Y. Li, “A dynamic model and some strategies on how to prevent and control hepatitis c in mainland China”, BMC Infectious Diseases, 19 (2019) 1.

D. A. Maimunah, “Mathematical model for HIV spreads control program with ART treatment”, Journal of Physics: Conference Series, 974 (2018) 1.

M. D. Miller-Dickson, V. A. Meszaros, S. Almagro-Moreno, C. B. Ogbunugafor, “Hepatitis C virus modelled as an indirectly transmitted infection highlights the centrality of injection drug equipment in disease[7] R. A. Frederick, C. B. Robert, “The dynamics of simultaneous infections with altered susceptibilities”, Theoretical Population Biology. 40 (1991) 369. dynamics”, Journal of Royal Society Interface, 16 (2019) 1.

G. Huang, Y. Takeuchi, “Global analysis on delay epidemiological dynamic models with nonlinear incidence”, Journal of Mathematical Biology, 63 (2011) 125.

Y. N. Krychko, K. B. Blyuss, “Global properties of a delayed SIR model with temporary immunity and nonlinear incidence rate”, Nonlinear analysis: Real world applications, 6 (2005) 495.

M. A. Safi, A. B. Gumel, “The effects of incidence functions on the dynamics of a quarantine/isolation model with time delay”, Nonlinear Analysis: Real World Applications, 12 (2011) 215.

Y.Wang, H.Wang,W. Jiang, “Stability switches and global Hopf bifurcation in a nutrient-plankton model”, Nonlinear Dynamics, 78 (2014) 981.

Y. Zhao, Z. Xu, “Global dynamics for a delayed Hepatitis C virus infection model”, Electronic Journal of differential equations, 2014 (2014) 1.

G. Huang, Y. Takeuchi, W. Ma, D.Wei, “Global stability for delay SIR & SEIR epidemic models with nonlinear incidence rate”, Bulletin of Mathematical Biology, 72 (2010).

S. Ruan, D. Xiao, J. C. Beier, “On the delayed Ross–Macdonald model for malaria transmission”, Bulletin of Mathematical Biology, 70 (2008) 4.

S. Barnerjee, R. Keval, S. Gakkhar, “Influence of intracellular delay on the dynamics of Hepatitis C virus”, International Journal of Applied and Computational Mathematics, 4 (2018) 1.

S. A. Gourley, Y. Kuang, J. D. Naggy, “Dynamics of a delay differential equation model of Hepatitis B virus infection”, Journal of Biological Dynamics, 2 (2008) 140.

J. K. Hale, Introduction to Functional Di erential Equations, Springer- Verlag, New York, 1993.

T. H. Gronwall, “Note on the derivatives with respect to a parameter of the solutions of a system of differential equations”, Annals of Mathematics, 20 (1919) 292.

E. Beretta, Y. Kuang, “Geometric stability switch criteria in delay differential systems with delay dependent parameters”, SIAM Journal of Mathematical Analysis, 33 (2002) 1144.

K. L. Cooke, P. van den Driessche, “On zeroes of some transcendental equations”, Funkcialaj Ekvacioj, 29 (1986) 77.

N. Hussaini, J. M.-S. Lubuma, K. Barley, A. B. Gumel, “Mathematical analysis of a model for AVL-HIV co-endemicity”, Mathematical Bioscience, 271 (2016) 80.

O. Y. Sharomi, Mathematical Analysis of Dynamics of Chlamydia trachomatis, PhD thesis, Department of Mathematics, University of Manitoba, Canada, 2010.

P. van den Driessche, J. Watmough, “Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission”, Mathematical Bioscience, 180 (2002) 29.

J. P. LaSalle, The Stability of Dynamical Systems, Regional Conference Series in Applied Mathematics, SIAM, Philadelphia, 1976.

R. Shi, Y. Cui, “Global analysis of a mathematical model for Hepatitis C virus transmissions”, Virus Research. 217 (2016) 17.

Z. Mukandavire, W. G.Chiyaka, “Asymptotic properties of an HIV/AIDS model with a time delay”, Journal of Mathematical Analysis and Applications 330 (2007) 933.

R. Shi, Y. Cui, “Global analysis of a mathematical model for Hepatitis C virus transmissions”, Virus Research. 217 (2016) 17. 11

Published

2021-02-16

How to Cite

Analysis of an HIV - HCV simultaneous infection model with time delay. (2021). Journal of the Nigerian Society of Physical Sciences, 3(1), 1-11. https://doi.org/10.46481/jnsps.2021.109

Issue

Volume 3, Issue 1, February 2021

Section

Original Research
Copyright & Licensing

The Journal of the Nigerian Society of Physical Sciences (JNSPS) is published under the Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0)4.0 (CC BY-NC) license. This license was developed to facilitate open access, namely, it allows articles to be freely downloaded and to be re-used and re-distributed without restriction, as long as the original work is correctly cited. More specifically, anyone may copy, distribute or reuse these articles, create extracts, abstracts, and other revised versions, adaptations or derivative works of or from an article, mine the article even for commercial purposes, as long as they credit the author(s).

How to Cite

Analysis of an HIV - HCV simultaneous infection model with time delay. (2021). Journal of the Nigerian Society of Physical Sciences, 3(1), 1-11. https://doi.org/10.46481/jnsps.2021.109