An Alleviation of Cloud Congestion Analysis of Fluid Retrial User on Matrix Analytic Method in IoT-based Application
Keywords:
Retrial queue, Stationary distribution, Congestion, Markov Fluid queue, Matrix analytic Method, IoT cloud computingAbstract
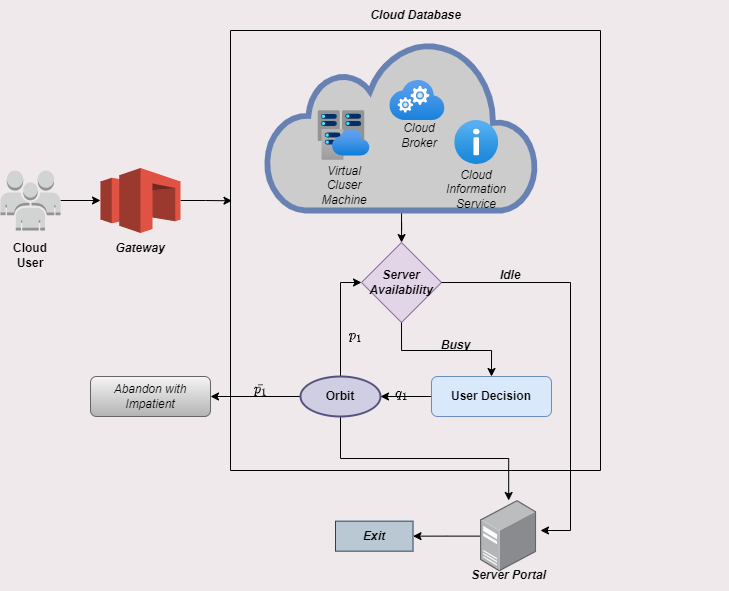
Cloud Computing (CC) and Internet of Things (IoT) are upgrowing human intervention to enhance the daily lifestyle. Currently, the heavy loaded traffic congestion is a very big challenge over IoT-based applications. For that purpose, the researchers approached various ways to overcome the congestion mechanism in recent years. Even though, they have futile to acheive the best resource storage accessing capacity expectation other than, Cloud Computing. Data sharing is a key impediment of Cloud Computing as well as Internet of Things. These are the constituent that give rise to the combination of the IoT and cloud computing paradigm as IoT Cloud. Though, preserving the missed data during the execution time is a key factor to indulge the Retrial Queueing Theory (RQT), who is facing issue upon accessing Cloud Service Provider (CSP) enter into virtual pool to preserve the data for reuse. The paper imposes Markov Fluid analysis with Matrix Analytic Method (MAM) allows the data as continuous length of data rather than individual data to avoid the congestion. The virtual orbit queue follow constant retrial rate discipline, that is, head of the orbital users makes attempt to occupy the server are assumed to be independent and identically distributed (i.i.d). Steady-state expression presented to study the behaviour of congestion. An illustrative analysis is produced to gain deep perception into the system model.
Published
How to Cite
Issue
Section
Copyright (c) 2023 K. Nandhini, V. Vidhya

This work is licensed under a Creative Commons Attribution 4.0 International License.







