Solving fractional variable-order differential equations of the non-singular derivative using Jacobi operational matrix

Authors

  • M. Basim Institute for Mathematical Research, Universiti Putra Malaysia, 43400 UPM, Serdang, Malaysia
  • N. Senu Institute for Mathematical Research, Universiti Putra Malaysia, 43400 UPM, Serdang, Malaysia | Department of Mathematics and statistics Universiti Putra Malaysia, 43400 UPM, Serdang, Malaysia
  • A. Ahmadian Decision Lab, Mediterranea University of Reggio Calabria, Reggio Calabria, Italy
  • Z. B. Ibrahim Department of Mathematics and statistics Universiti Putra Malaysia, 43400 UPM, Serdang, Malaysia
  • S. Salahshour Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey

Keywords:

FDEs; Non-singular derivative; Variable order; Operational matrix.

Abstract

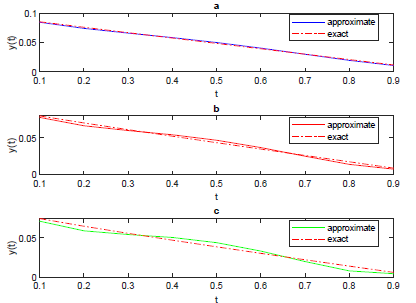
This research derives the shifted Jacobi operational matrix (JOM) with respect to fractional derivatives, implemented with the spectral tau method for the numerical solution of the Atangana-Baleanu Caputo (ABC) derivative. The major aspect of this method is that it considerably simplifies problems by reducing them to ones that can be solved by solving a set of algebraic equations. The main advantage of this method is its high robustness and accuracy gained by a small number of Jacobi functions. The suggested approaches are applied in solving non-linear and linear ABC problems according to initial conditions, and the efficiency and applicability of the proposed method are proved by several test examples. A lot of focus is placed on contrasting the numerical outcomes discovered by the new algorithm together with those discovered by previously well-known methods.

Dimensions

K. S. Miller, & B. Ross, “An introduction to the fractional calculus and fractional differential equations”, Wiley, (1993).

K. Oldham, & J. Spanier, “The fractional calculus theory and applications of differentiation and integration to arbitrary order”, Elsevier, (1974).

M. Amairi, M. Aoun, S. Najar & M. N. Abdelkrim, “A constant enclosure method for validating existence and uniqueness of the solution of an initial value problem for a fractional differential equation”, Applied Mathematics and Computation 217 (2010) 2162.

J. Deng, & L. Ma, “Existence and uniqueness of solutions of initial value problems for nonlinear fractional differential equations”, Applied Mathematics Letters 23 (2010) 676.

L. K. Alzaki, & H. K. Jassim, “Time-Fractional Differential Equations with an Approximate Solution”, Journal of the Nigerian Society of Physical Sciences (2022) 818.

O. A. Uwaheren, A. F. Adebisi, & O. A. Taiwo, “Perturbed collocation method for solving singular multi-order fractional differential equations of Lane-Emden type”, Journal of the Nigerian Society of Physical Sciences (2020) 141.

K. M. Owolabi, & A. Atangana, “On the formulation of Adams-Bashforth scheme with Atangana-Baleanu-Caputo fractional derivative to model chaotic problems”, Chaos: An Interdisciplinary Journal of Nonlinear Science 29 (2019) 023111.

S. Arshad, I. Saleem, O. Defterli, Y. Tang, & D. Baleanu, “Simpson’s method for fractional differential equations with a non-singular kernel applied to a chaotic tumor model”, Physica Scripta 96 (2021) 124019.

S. Qureshi, & A. Yusuf, “Modeling chickenpox disease with fractional derivatives: From caputo to atangana-baleanu.” Chaos, Solitons & Fractals 122 (2019) 111.

I. Ahmed, E. F. D. Goufo, A. Yusuf, P. Kumam, P. Chaipanya, & K. Nonlaopon, “An epidemic prediction from analysis of a combined HIVCOVID-19 co-infection model via ABC-fractional operator”, Alexandria Engineering Journal 60 (2021) 2979.

S. Djennadi, N. Shawagfeh, M. S. Osman, J. F. Gomez-Aguilar, & O.´ A. Arqub, “The Tikhonov regularization method for the inverse source problem of time fractional heat equation in the view of ABC-fractional technique”, Physica Scripta 96 (2021) 094006.

A. Saadatmandi, & M. Dehghan, “A new operational matrix for solving fractional-order differential equations”, Computers & mathematics with applications 59 (2010) 1326.

E. H. Doha, A. H. Bhrawy, & S. S. Ezz-Eldien, “Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations”, Applied Mathematical Modelling 35 (2011) 5662.

A. H. Bhrawy, A. S. Alofi, & S. S. Ezz-Eldien, “A quadrature tau method for fractional differential equations with variable coefficients”, Applied Mathematics Letters 24 (2011) 2146.

E. H. Doha, A. H. Bhrawy, & S. S. Ezz-Eldien, “A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order”, Computers & Mathematics with Applications 62 (2011) 2364.

F. Ghoreishi, & S. Yazdani, “An extension of the spectral Tau method for numerical solution of multi-order fractional differential equations with convergence analysis”, Computers & Mathematics with Applications 61 (2011) 30.

S. K. Vanani, & A. Aminataei, “Tau approximate solution of fractional partial differential equations”, Computers & Mathematics with Applications 62 (2011) 1075.

A. Pedas, & E. Tamme, “On the convergence of spline collocation methods for solving fractional differential equations”, Journal of Computational and Applied Mathematics 235 (2011) 3502.

S. Esmaeili, & M. Shamsi, “A pseudo-spectral scheme for the approximate solution of a family of fractional differential equations”, Communications in Nonlinear Science and Numerical Simulation 16 (2011) 3646.

S. Esmaeili, M. Shamsi, & Y. Luchko, “Numerical solution of fractional differential equations with a collocation method based on Muntz polyno-¨ mials”, Computers & Mathematics with Applications 62 (2011) 918.

G. Szego, “Am. Math. Soc. Colloq. Pub. 23”, Orthogonal Polynomials¨ (1985).

E. H. Doha, A. H. Bhrawy, & R. M. Hafez “A Jacobi dual-Petrov-Galerkin method for solving some odd-order ordinary differential equations”, Abstract and Applied Analysis 2011 (2011).

E. H. Doha, A. H. Bhrawy, & S. S. Ezz-Eldien, “A new Jacobi operational matrix: an application for solving fractional differential equations”, Applied Mathematical Modelling 36 (2012) 4931.

E. H. Doha, “On the construction of recurrence relations for the expansion and connection coefficients in series of Jacobi polynomials”, Journal of Physics A: Mathematical and General 37 (2004) 657.

Y. L. Luke, “The special functions and their approximations”, 53 (1969).

M. Basim, N. Senu, Z. B. Ibrahim, A. Ahmadian, & S. Salahshour, “a Robust Operational Matrix of Nonsingular Derivative to Solve Fractional Variable-Order Differential Equations”, Fractals 30 (2022) 2240041.

J. D.Djida, A. Atangana, & I. Area, “Numerical computation of a fractional derivative with non-local and non-singular kernel”, Mathematical Modelling of Natural Phenomena 12 (2017) 4.

M. Toufik, & A. Atangana, “New numerical approximation of fractional derivative with non-local and non-singular kernel: application to chaotic models”, The European Physical Journal Plus 132 (2017) 1.

M.Caputo, & M. Fabrizio, “A new definition of fractional derivative without singular kernel”, Progress in Fractional Differentiation & Applications 1 (2015) 73.

A. Atangana, & D. Baleanu, “New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model”, arXiv preprint arXiv:1602.03408 (2016).

X. Li, Y. Gao, & B. Wu, “Approximate solutions of Atangana-Baleanu variable order fractional problems”, AIMS Mathematics 5 (2020) 2285.

L. J. Rong, & P. Chang, “Jacobi wavelet operational matrix of fractional integration for solving fractional integro-differential equation”, Journal of Physics: Conference Series 693 (2016) 012002.

C. Phang, Y. T. Toh, & F. S. Md Nasrudin, “An operational matrix method based on poly-Bernoulli polynomials for solving fractional delay differential equations”, Computation 8 (2020) 82.

S. Salahshour, A. Ahmadian, M. Salimi, M. Ferrara, & D. Baleanu, “Asymptotic solutions of fractional interval differential equations with nonsingular kernel derivative”, Chaos: An Interdisciplinary Journal of Nonlinear Science 29 (2019) 083110.

A. Al-Rabtah, S. Momani, & M. A. Ramadan, “Solving linear and nonlinear fractional differential equations using spline functions”, Abstract and Applied Analysis 2012 (2012).

Z. M. Odibat, & S. Momani, “An algorithm for the numerical solution of differential equations of fractional order”, Journal of Applied Mathematics & Informatics 26 (2008) 15.

A. Al-Rabtah, S. Momani, & M. A. Ramadan, “Solving linear and nonlinear fractional differential equations using spline functions”, Abstract and Applied Analysis 2012 (2012).

X. Li, Y. Gao, & B. Wu, “Approximate solutions of Atangana-Baleanu variable order fractional problems”, AIMS Mathematics 5 (2020) 2285.

D. Baleanu, “Approximate solutions for solving nonlinear variable-order fractional Riccati differential equations”, Inst Mathematics & Informatics (2019).

Published

2023-05-05

How to Cite

Solving fractional variable-order differential equations of the non-singular derivative using Jacobi operational matrix. (2023). Journal of the Nigerian Society of Physical Sciences, 5(2), 1221. https://doi.org/10.46481/jnsps.2023.1221

Issue

Volume 5, Issue 2, May 2023

Section

Original Research
Copyright & Licensing

Copyright (c) 2023 M. Basim, N. Senu, A. Ahmadian, Z. B. Ibrahim

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Solving fractional variable-order differential equations of the non-singular derivative using Jacobi operational matrix. (2023). Journal of the Nigerian Society of Physical Sciences, 5(2), 1221. https://doi.org/10.46481/jnsps.2023.1221