Efficient Hybrid Block Method For The Numerical Solution Of Second-order Partial Differential Problems via the Method of Lines

Authors

  • Olumide O. Olaiya
    Department of Mathematics Programme, National Mathematical Centre, Abuja, Nigeria
  • Rasaq A. Azeez
    Department of Mathematics, University of Abuja, Abuja, Nigeria
  • Mark I. Modebei
    Department of Mathematics Programme, National Mathematical Centre, Abuja, Nigeria

Keywords:

Initial Value Problem, Boundary Value Problem, Block method, Linear Multistep Method, Hybrid method, mehod od lines

Abstract

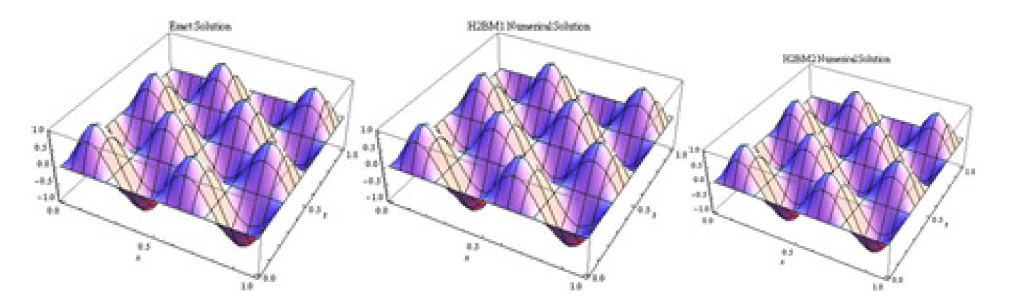
This study is therefore aimed at developing classes of efficient numerical integration schemes, for direct solution of second-order Partial Differential Equations (PDEs) with the aid of the method of lines. The power series polynomials were used as basis functions for trial solutions in the derivation of the proposed schemes via collocation and interpolation techniques at some appropriately chosen grid and off-grid points the derived
schemes are consistent, zero-stable and convergent. the proposed methods perform better in terms of accuracy than some existing methods in the literature.

Dimensions

L. Brugnano, L. & D. Trigiante, “Solving Differential Problems by Multistep Initial and Boundary Value Methods".Gordon and Breach Science Publishers (1998), Amsterdam.

P. Onumanyi, U.W. Sirisena. & S.N Jator, “Continuous finite difference ap-

proximations for solving differential equations”, International. Journal of. Computer Mathematics. 72 (1999) 15-27.

P. Onumanyi, D. O. Awoyemi, S. N. Jator & U. W. Sirisena, “New linear

mutlistep methods with continuous coeffcients for first order initial value problems”,

Journal of. Nigeria. Mathematics. Society. 13, (1994), 37-51.

S. N. Jator “On the Hybrid Method with Three-Off Step Points for Initial Value Problems” International Journal of Mathematical Education in Science and Technology, 41, (2010), 110-118 http://dx.doi.org/10.1080/00207390903189203

S. N. Jator “Trigonometric symmetric boundary value method for oscillating solutions including the sine-Gordon and Poisson equations” Cogent Mathematics 3 (2016), 1271269

S. O. Fatunla, “Block Methods for second-order IVP”, International Journal of Mathematics 55, (1999)

Y. Yusuph & P. Onumanyi; “New multiple FDM through multistep collocation for y^''=f(x,y)” Proceedings of the conference, National Mathematical Centre, Abuja (2005).

Siraj-ul-Islam, Imran Aziz & Bozidar Sarler, “The numerical solution of second-order boundary-value problems by collocation method with the Haar wavelets”, Mathematical and Computer Modelling 52 (2010) 1577-1590.

J. Adewale, A. Olaide. & J. Sunday, “Continuous Block Method for the Solution of second rder Initial Value Problems of Ordinary Diff. Equation” International Journal of Pure and Applied mathematics 82, (2013), 405-416.

F.F. Ngwane & S. N. Jator, “L-Stable Block Hybrid Second Derivative Algorithm for Parabolic Partial Differential Equations”. American Journal of Computational Mathematics, 4, (2014) 87-92. http://dx.doi.org/10.4236/jasmi.2014.42008

J. Vigo-Aguiar & H. Ramos, “A family of A-Stable Collocation Methods of Higher Order for Initial-Value Problems”. IMA Journal of Numerical Analysis, 27, (2007), 798-817. http://dx.doi.org/10.1093/imanum/drl040

J. R, Cash “Two New Finite Difference Schemes for Parabolic Equations”. SIAM Journal of Numerical Analysis, 21, (1984) 433-446. http://dx.doi.org/10.1137/0721032

S. N. Jator & J. Li, “An algorithm for Second Order Initial and Boundary Value Problems” Numerical Algorithm (2012), 59-67

T. A. Biala, “Computational Study of the Boundary Value Methods and the Block Unification Methods for y''=f(x,y,y')”, Abstract and Applied Analysis 2016, Article ID 8465103, 14 pages http://dx.doi.org/10.1155/2016/8465103

P. Henrici, “Discrete Variable Methods in Ordinary Differential Equations”, John Wiley, New York, 1962.

] J. D. Lambert, “Computational Methods in in Ordinary Differential Equations” :John Wiley and Sons, New York, NY, USA, 1973;

M. I. Modebei, R. B. Adeniyi, S. N. Jator & H. C. Ramos “A block hybrid integrator for numerically solving fourth-order Initial Value Problems” Applied Mathematics and Computation 346, (2019), 680-694

Published

2021-02-25

How to Cite

Efficient Hybrid Block Method For The Numerical Solution Of Second-order Partial Differential Problems via the Method of Lines. (2021). Journal of the Nigerian Society of Physical Sciences, 3(1), 26-37. https://doi.org/10.46481/jnsps.2021.140

Issue

Volume 3, Issue 1, February 2021

Section

Original Research
Copyright & Licensing

Copyright (c) 2021 Journal of the Nigerian Society of Physical Sciences

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Efficient Hybrid Block Method For The Numerical Solution Of Second-order Partial Differential Problems via the Method of Lines. (2021). Journal of the Nigerian Society of Physical Sciences, 3(1), 26-37. https://doi.org/10.46481/jnsps.2021.140

Similar Articles

1-10 of 358

You may also start an advanced similarity search for this article.

Most read articles by the same author(s)