Dynamics of Toxoplasmosis Disease in Cats population with vaccination

https://doi.org/10.46481/jnsps.2021.141

Authors

  • Idris Babaji Muhammad Department of Mathematics ,Faculty of Science, Bauchi State University, Gadau P.M.B65,Gadau, Nigeria
  • Salisu Usaini Department of Mathematics , Kano University of Science and Technology, Wudil, P.M.B. 3244, Kano, Nigeria

Keywords:

Toxoplasmosis, Vaccination, Cats, Sensitivity index

Abstract

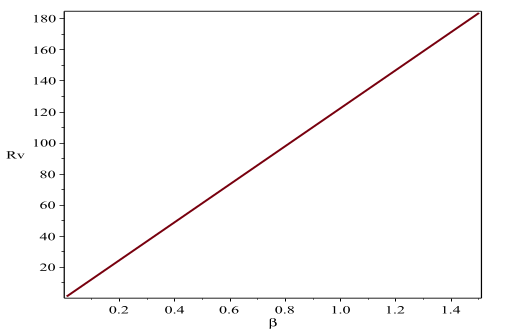
We extend the deterministic model for the dynamics of toxoplasmosis proposed by Arenas et al. in 2010, by separating vaccinated and recovered classes. The model exhibits two equilibrium points, the disease-free and endemic steady states. These points are both locally and globally stable asymptotically when the threshold parameter Rv is less than and greater than unity, respectively. The sensitivity analysis of the model parameters reveals that the vaccination parameter $\pi$ is more sensitive to changes than any other parameter. Indeed, as expected the numerical simulations reveal that the higher the vaccination rate of susceptible individuals the smaller the value of the threshold Rv (i.e., increase in $\pi$ results in the decrease in Rv , leading to the eradication of toxoplasmosis in cats population.

Dimensions

A. Gautam & A. Priyadarshi, “Mathematical Modelling of Toxoplasma Gondii and Host Immune Response”, AIP Conference Proceedings 1975 (2018) 030002, doi: 10.1063/1.5042172.

A. J. Arenas, G. Gonzlez-Parra & R. J. “Villanueva Mic, Modeling toxoplasmosis spread in cat populations under vaccination”, Theor. Popul. Biol. 77 (2010) 227, https://doi.org/10.1016/j.tpb.2010.03.005.

C. Castillo-Chavez & B. Song, “Dynamical models of tuberculosis and their applications”, Math. Biosci. Engin. 1 (2004) 361, doi:10.3934/mbe.2004.1.361.

C. Peña & K. G. Hermes Martinez, “Hybrid model of the spread of Toxoplasmosis between two Town of Colombia”, Tecciencia 7 (2015) 1, DOI:http:/dx.doi.org/10.18180/tecciencia.2015.18.1.

C. Ramakrishnan, S. Maier, R. A. Walker, H. Rehrauer, et al., “An experimental genetically attenuated live vaccine to prevent transmission of Toxoplasma gondii by cats”, Scientific Reports 9 (2019) 1479,

https://doi.org/10.1038/s41598-018-37671-8.

D. F. Aranda, R. J. Villanueva, A. J. Arenas & G. C. Gonzalez-Parra, “Mathematical modeling of Toxoplasmosis disease in varying size populations”, Comp. Math. Appl. 56 (2008) 690, https://doi.org/10.1016/j.camwa.2008.01.008.

D. L. Zulpo, A. S. Sammi, J. R. dos Santos, et al., “Toxoplasma gondii: A study of oocyst re-shedding in domestic cats”, J. Vet. Parasitol. 249 (2018) 17.

E. A. Innes, P. M. Bartley, S. Maley, F. Katzer & D. Buxton, “Veterinary vaccines against Toxoplasma gondii, Mem Inst Oswaldo Cruz”, Rio de Janeiro 104 (2009) 246.

G. C. Gonzlez-Parra, A. J. Arenas, D. F. Aranda, R. J. Villanueva & L. Jdar, “Dynamics of a model of Toxoplasmosis disease in human and cat populations”, Comp.Math. Appl. 57 (2009) 1692,

https://doi.org/10.1016/j.camwa.2008.09.012.

J. A. Le ón Mar ín & I. D. Gandica, “A mathematical model for the reproduction dynamics of toxoplasma gondii”, J. Biol. Syst. 23 (2015) S91, doi: 10.1142/S0218339015400082.

J. D. Ferreira, L. M. Echeverry & C. A. Pea Rincon, “Stability and bifurcation in epidemic models describing the transmission of toxoplasmosis in human and cat populations”, Math. Meth. Appl. Sci. 40 (2017) 5575, doi: 10.1002/mma.4410.

J. P. Dubey, “The history of Toxoplasma gondii: The first 100 years”, J. Eukaryot. Microbiol. 55 (2008) 467, doi: 10.1111/j.1550-7408.2008.00345.x.

K. M. Addo, “SEIR Model for Dogs Rabies. A case study: Bango District, Ghana”, Master’s thesis, Kwame Nkurumah University of Science and Technology, Ghana (2012).

K. Sornsong, S. Naowarat & P. Thongjaem, “Mathematical model for the dynamics transmission of rabies with control measures”, Austr. J. Basics and Appl. Sci. 10 (2016) 169.

M. Hari & Y. Zulfahmi, “Bifurcation Analysis of Toxoplasmosis Epidemic Control on Increased Controlled Rate of Suppressing the Rate of Infected Births”, Int. J. Comp. Sci. Appl. Math. 6 (2020) 1, doi:10.12962/j24775401.v6i1.5978.

M. Langlais, M. Llu, C. Avenet & E. Gilot-Fromont, “A simplified model system for Toxoplasma gondii spread within a heterogeneous environment”, Nonlinear Dyn. 68 (2012) 381, doi:10.1007/s11071-011-0255-4.

N. Chitnis, J. M. Hyman & J. M. Cushing, “Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model”, Bull. Math. Biol. 70 (2008) 1272, doi:10.1007/s11538-008-9299-0.

O. M. Ogunmiloro, “Mathematical Modeling of the Coinfection Dynamics of Malaria-Toxoplasmosis in the Tropics”, Biomet. Lett. 56 (2019) 139, doi: https://doi.org/10.2478/bile-2019-0013.

P. Glendinning, Stability, Instability and Choas: an introduction to the theory of nonlinear differential equations, Cambridge University Press, (1994).

P. Van den Driessche & J. Wanmough, “Reproduction numbers and subthreshold endemic equilibria for compartimental models of disease transmition”, Mathematical Biosciences 180 (2000) 29.

R. Verma & P. Khanna, “Development of Toxoplasma gondii vaccine: A global challenge”, Human Vac. Imm. therap. 9 (2013) 291.

S.M. Garba, A.B. Gumel & M.R. Abu Bakar, “Backward bifurcations in dengue transmission dynamics”, Math. Biosci. 215 (2008) 11.

S. Usaini, U. T. Mustapha & S. M. Sabiu, “Modelling scholastic underachievement as a contagious disease”, Math. Meth. Appl. Sci. Special Issue (2018) 1, https://doi.org/10.1002/mma.4924.

T. Loung & S. A. Davis, “Rabies vaccination targets for stray dogs population”, Frontiers in Vet. Sci. 4 (2017) 52.

T. Dubie, G. Terefe, M. Asaye & T. Sisay , “Toxoplasmosis: Epidemiology with the emphasis of its public health importance” 2 (2014) 097.

Published

2021-02-18

How to Cite

Dynamics of Toxoplasmosis Disease in Cats population with vaccination. (2021). Journal of the Nigerian Society of Physical Sciences, 3(1), 17-25. https://doi.org/10.46481/jnsps.2021.141

Issue

Volume 3, Issue 1, February 2021

Section

Original Research
Copyright & Licensing

The Journal of the Nigerian Society of Physical Sciences (JNSPS) is published under the Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0)4.0 (CC BY-NC) license. This license was developed to facilitate open access, namely, it allows articles to be freely downloaded and to be re-used and re-distributed without restriction, as long as the original work is correctly cited. More specifically, anyone may copy, distribute or reuse these articles, create extracts, abstracts, and other revised versions, adaptations or derivative works of or from an article, mine the article even for commercial purposes, as long as they credit the author(s).

How to Cite

Dynamics of Toxoplasmosis Disease in Cats population with vaccination. (2021). Journal of the Nigerian Society of Physical Sciences, 3(1), 17-25. https://doi.org/10.46481/jnsps.2021.141