Comments on “The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method: J. Nig. Soc. Phys. Sci. 1 (2019) 82-87”

Authors

  • Gurpreet Tuteja Zakir Husain Delhi College, University of Delhi
  • Tapshi Singh Satyawati College, University of Delhi

Keywords:

SIR model, Differential Transformation Method (DTM), Dengue Fever, Treatment

Abstract

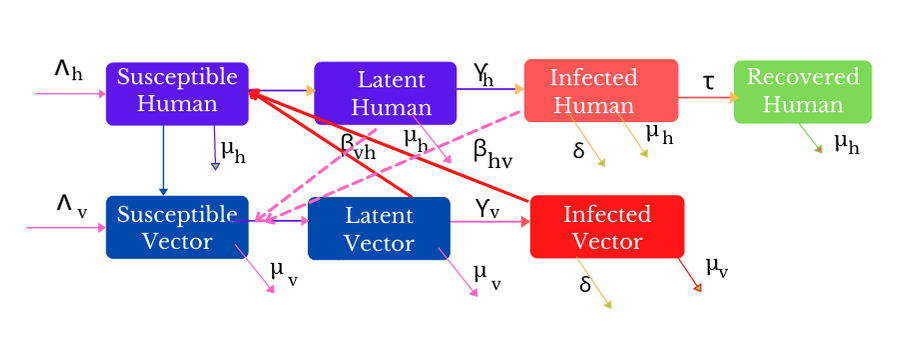
The mathematical model for dengue fever transmission studied by [1], has been re-investigated. The differential transformation method (DTM) is used to compute the semi-analytical solutions of the non-linear differential equations of the compartment (SIR) model of dengue fever. This epidemiology problem is well-posed. The effect of treatment as a control measure is studied through the growth equations of exposed and infected humans. The inadvertent errors in the recurrence relations (DTM) of equations for dengue disease transmission including initial conditions have been removed. Furthermore, the semi-analytic solutions of the model are obtained and verified with the built-in function AsymptoticDSolveValue of Wolfram Mathematica. It has been found that results obtained from the DTM are valid only for small-time t (t < 1.5), as t becomes large, the human population (exposed and recovered) and infected vector population become negative.

Dimensions

F. Y. Eguda, A. James & S. Babuba, The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method, Journal of Nigerian Society of Physical Sciences 1 (2019) 82.

Dengue. Retrieved from World Health Organization: https://www.who.int/immunization/diseases/dengue/en/(2021)

Dengue-and-Severe-Dengue. Retrieved from World Health Organization: https://www.who.int/news-room/fact-sheets/detail/dengue-and-severe dengue (2021).

A. Mathieu, N Hens, C Marais & B P Beutels, Dynamic Epidemiological Models for Dengue PLOSONE 7 (2012) 1.

Messina, J. P., Brady, O. J., Golding, N., Kraemer .et.al. The current and future global distribution and the population at risk of dengue. Nature Microbiology 4 (2019), 15081515.

V Capasso & G Serio, A generalization of the Kermack-McKendrick deterministic epidemic model, Mathematical Biosciences 42 (1978) 43.

W. O. Kermack & MA. G. McKendrick, Contribution to the Mathematical Theory of Epidemics (Part 1). Proceedings of Royal Society London 138A (1932) 55.

W. O. Kermack & MA. G. McKendrick, Contribution to the Mathematical Theory of Epidemics (Part II), Proceedings of Royal Society London 141 (1932) 94.

W. O. Kermack & MA. G. McKendrick, A contribution to the mathematical theory of epidemics, Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Science 115 (1927), 700.

H Hethcote, The Mathematics of Infectious Diseases, SIAM Review, 42 (2000) 599.

J K Zhou, Differential Transformation and Its Applications for Electrical Circuits, Huazhong University Press, China 1986.

P Olumuyiwa et. al. Direct and Indirect Transmission Dynamics of Typhoid Fever Model by Differential Transform Method, ATBU Journal of Science, Technology and Education, 6 (2018) 167.

P. Olumuyiwa & M O. Ibrahim, Application of Differential Transform Method in Solving a Typhoid Fever Model, International Journal Of Mathematical Analysis And Optimization: Theory And Applications 1 (2017) 250.

A. Abioye, M. O. Ibrahim, O. Peter, A. Sylvanus & F. Abiodun, Differential Transform Method for Solving Mathematical Model of SEIR and SEI Spread of Malaria, International Journal of Sciences: Basic and Applied

Research 40 (2018) 197.

J. A. Abraham, G. P. Gilberto & Benito M. Chen-Charpentier, Dynamical analysis of the transmission of seasonal diseases using the differential transformation method, Mathematical and Computer Modelling 50 (2009), 765.

M. Derouich & A. Boutayeb, Dengue fever: Mathematical modelling and computer simulation, Applied Mathematics and Computation 177 (2006) 528.

Z. N. Meksianis, N Anggriani & A. K. Supriatna, Application of differential transformation method for solving dengue transmission mathematical model, AIP Conference Proceedings 2018.

N. R. Derrick & S. L. Grossman, “Differential Equation with applications”, Addison Wesley Publishing Company Inc., Philippines 1976.

Published

2021-05-29

How to Cite

Comments on “The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method: J. Nig. Soc. Phys. Sci. 1 (2019) 82-87”. (2021). Journal of the Nigerian Society of Physical Sciences, 3(2), 82-88. https://doi.org/10.46481/jnsps.2021.170

Issue

Volume 3, Issue 2, May 2021

Section

Original Research
Copyright & Licensing

Copyright (c) 2021 Journal of the Nigerian Society of Physical Sciences

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Comments on “The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method: J. Nig. Soc. Phys. Sci. 1 (2019) 82-87”. (2021). Journal of the Nigerian Society of Physical Sciences, 3(2), 82-88. https://doi.org/10.46481/jnsps.2021.170