An Investor’s Investment Plan with Stochastic Interest Rate under the CEV Model and the Ornstein-Uhlenbeck Process
Keywords:
O-U process, Stochastic interest rate, Optimal investment plan, Legendre transform, CEV modelAbstract
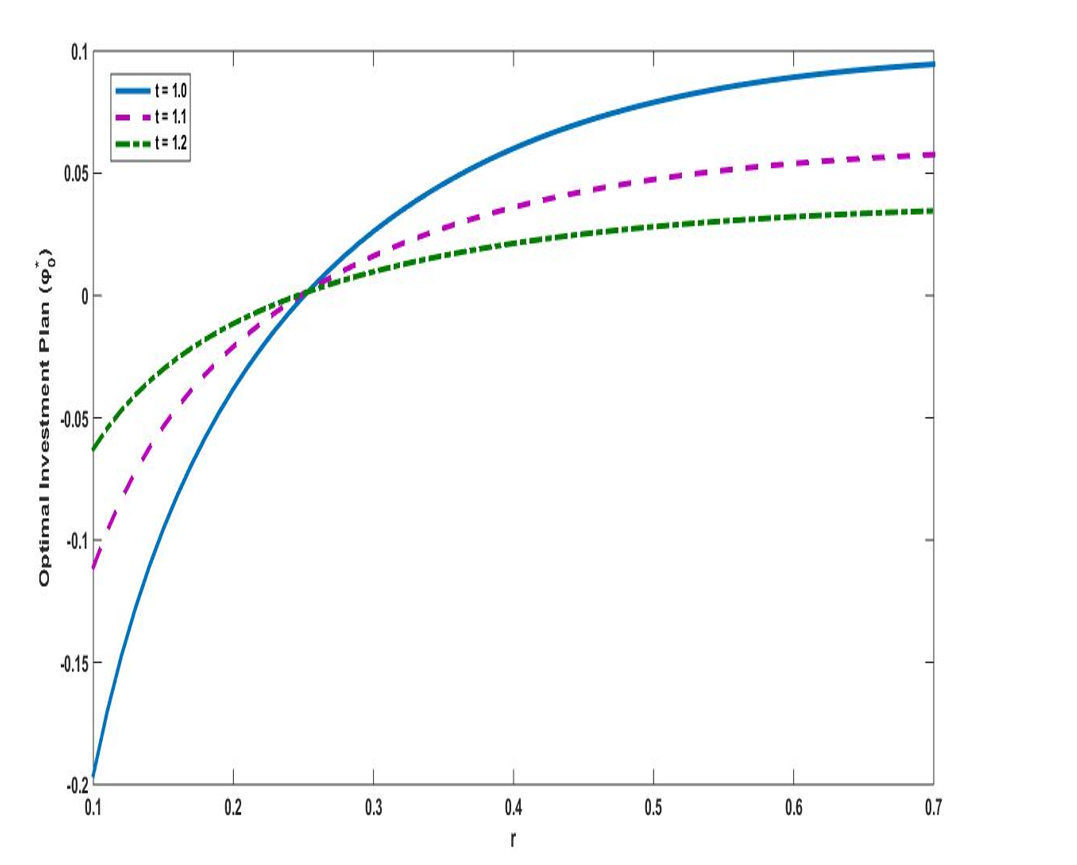
The aim of this paper is to maximize an investor’s terminal wealth which exhibits constant relative risk aversion (CRRA). Considering the fluctuating nature of the stock market price, it is imperative for investors to study and develop an effective investment plan that considers the volatility of the stock market price and the fluctuation in interest rate. To achieve this, the optimal investment plan for an investor with logarithm utility under constant elasticity of variance (CEV) model in the presence of stochastic interest rate is considered. Also, a portfolio with one risk free asset and two risky assets is considered where the risk free interest rate follows the Ornstein-Uhlenbeck (O-U) process and the two risky assets follow the CEV process. Using the Legendre transformation and dual theory with asymptotic expansion technique, closed form solutions of the optimal investment plans are obtained. Furthermore, the impacts of some sensitive parameters on the optimal investment plans are analyzed numerically. We observed that the optimal investment plan for the three assets give a fluctuation effect, showing that the investor’s behaviour in his investment pattern changes at different time intervals due to some information available in the financial market such as the fluctuations in the risk free interest rate occasioned by the O-U process, appreciation rates of the risky assets prices and the volatility of the stock market price due to changes in the elasticity parameters. Also, the optimal investment plans for the risky assets are directly proportional to the elasticity parameters and inversely proportional to the risk free interest rate and does not depend on the risk averse coefficient.
Published
How to Cite
Issue
Section
Copyright (c) 2021 Journal of the Nigerian Society of Physical Sciences

This work is licensed under a Creative Commons Attribution 4.0 International License.







