A study of growth of COVID-19 with super-spreaders using the modified SIR model including iceberg phenomenon

Gurpreet Singh Tuteja; Tapshi Lal

doi:10.46481/jnsps.2024.1828

Authors

Gurpreet Singh Tuteja Zakir Husain Delhi College, University of Delhi, Delhi, India
Tapshi Lal
tapshisingh@ymail.com
Satyawati College, University of Delhi, Delhi, India

Keywords:

SIR model, COVID-19, Super-spreaders, Super Spreading Event, Iceberg phenomenon in epidemiology, Basic reproduction number

Abstract

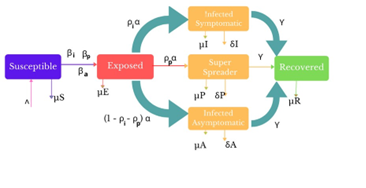
This paper explores the dynamics of COVID-19 transmission, particularly focusing on super-spreaders, through the lens of the SIR model. The model comprises six compartments representing susceptible, exposed, symptomatic infected, super-spreader, asymptomatic infected, and recovered individuals. Utilizing a set of non-linear, interdependent differential equations, we numerically solve for model parameters to examine the influence of super-spreaders on infection spread within the population. We calculate the basic reproduction number (R₀) and discuss the stability of disease-free equilibrium. Our findings underscore the significant role played by super-spreaders and asymptomatic individuals in disease dissemination. Drawing on the epidemiological concept of the iceberg phenomenon, we offer insights into super-spreader events (SSEs) in India and their ramifications.

Dimensions

REFERENCES

W. O. Kermack & A. G. McKendrick,“A contribution to the mathematical theory of epidemics”, Proceedings of the Royal Society of London A: Mathematical, physical and engineering science 115 (1927) 700. https://doi.org/10.1098/rspa.1927.0118.

COVID-19 Transmission, European Centre for Disease Prevention and Control, 2021. https://www.ecdc.europa.eu/en/COVID-19/ latest-evidence/transmission.

A. Aggarwal & R. Bhardwaj, “Probability of COVID-19 infection by the cough of a normal person and a super-spreader”, Physics of Fluids 33 (2021) 031704. https://doi.org/10.1063/5.0041596.

J. Aguilar & J. Gutierrez, “Investigating the Impact of Asymptomatic Carriers on COVID-19 Transmission”, medRxiv (2020) 1. https://doi.org/10.1101/2020.03.18.20037994.

L. S. Huang, L. Li, L. Dunn & M. He, “Taking account of asymptomatic infections: A modelling study of the COVID-19 outbreak on the Diamond Princess cruise ship”, PLoS One 16 (2021) 1. https://doi.org/10.1371/journal.pone.0248273.

J. Lin, K. Yan, J. Zhang, T. Cai & J. Zheng, “A super-spreader of COVID19 in Ningbo city in China”, J. Infect Public Health 13 (2020) 935. https://doi.org/10.1016/j.jiph.2020.05.023.

T. R. Frieden & C. T. Lee, “Identifying and Interrupting Super spreading Events- Implications for Control of Severe Acute Respiratory Syndrome Coronavirus 2”, Emerging Infectious Diseases 26(6) (2020) 1059. https://doi.org/10.3201/eid2606.200495.

J. L. Smith, S. Schreiber, P. Kopp, W. M. Getz, “Superspreading and the effect of individual variation on disease emergence”, Nature 438(7066) (2005) 355. https://doi.org/10.1038/nature04153.

R. A. Stein, “Super-spreaders in infectious diseases”, International Journal of Infectious Diseases 15 (2011) 510. https://doi.org/10.1016/j.ijid.2010.06.020.

L. Cooper, S. Y. Kang, D. Bisanzio, et al., “Pareto rules for malaria superspreaders and super-spreading”, Nature Communication 10 (2019) 3939. https://doi.org/10.1038/s41467-019-11861-y

D. Kumar, D. S. Meena, M. K. Garg & S. Misra, “Super-spreader resurgence in COVID-19: Past encounters and future repercussion”, Journal of Family Medicine and Primary Care 9 (2020) 5404. https://doi.org/10.4103/jfmpc.jfmpc_1112_20.

D. Majra, J. Benson, J. Pitts & J. Stebbing, “SARS-CoV-2 (COVID-19) superspreader events”, Journal of Infection 82 (2021) 36. https://doi.org/10.1016/j.jinf.2020.11.021

V. Capasso & G. Serio, “A generalization of the Kermack-Mckendrick deterministic epidemic model”, Mathematical Bio-sciences 42 (1978) 43. https://doi.org/10.1016/0025-5564(78)9006-8.

W. O. Kermack & A. G. McKendrick, “Contribution to the Mathematical Theory of Epidemics (Part II)”, Proc. R. Soc. Lond. B. Biol. Sci. 138 (1932) 55. https://doi.org/10.1098/rspa.1932.0171.

W. O. Kermack & A. G. McKendrick, “Contribution to the Mathematical Theory of Epidemics (Part III)”, Proc. R. Soc. Lond. B. Biol. Sci. 141 (1932) 94. https://doi.org/10.1098/rspa.1933.0106.

H. W. Hethcote & A. L. Simon, Periodicity in epidemiological models, in H. T. Gross L., Applied Mathematical Ecology, Springer-

Verlag, Berlin,1989, pp.193. https://link.springer.com/chapter/10.1007/978-3-642-61317-3 8.

H. W. Hethcote & P. van den Driessche, “Some epidemiological models with nonlinear incidence”, Journal of Mathematical Biology 29 (1997) 271. https://doi.org/10.1007/BF00160539.

H. Hethcote, “The Mathematics of Infectious Diseases”, SIAM Review 42 (2000) 599. https://doi.org/10.1137/S0036144500371907.

W. R. Derrick, “A disease transmission model in a non-constant population”, Journal of Mathematical Biology 31 (1993) 495. https://doi.org/10.1007/BF00173889

Y. C. Chen, P. E. Lu, C. S. Chang & T. H. Liu, “A Time-Dependent SIR Model for COVID-19 with Undetectable Infected Persons”, IEEE Transactions on Network Science and Engineering 7 (2020) 3279. https://doi.org/10.1109/TNSE.2020.3024723.

F. Nda¨?rou, I. Area, J. J. Nieto & F. M. Delfim, “Mathematical modelling of COVID-19 transmission dynamics with a case study of Wuhan”, Chaos Solitons Fractals 135 (2020) 109846. https://doi.org/10.1016/j.chaos.2020.109846.

N. R. Derrick, Differential equation with applications, Philippines: Addision Wesley Publishing Company, Inc., 1976. https://cir.nii.ac.jp/crid/1130282272562414464

G. S. Tuteja & T. Lal, “Comments on “The solution of a mathematical model for dengue fever transmission using differential transformation method””, J. Nig. Soc. Phys. Sci. 3 (2021) 82. https://doi.org/10.46481/ jnsps.2021.170.

R. M. Anderson & R. M. May, “Infectious disease of Humans: dynamics and control”, Oxford University Press, 1992.

G. G. Katul, A. Mrad, S. Bonetti, G. Manoli & A. J. Parolari, “Global convergence of COVID- 19 basic reproduction number and estimation from early-time SIR dynamics”, PLOS ONE 15 (2020) 0239800. https://doi.org/10.1371/journal.pone.0239800.

G. Magombedze, C. N. Ngonghala & C. Lanzas, “Evolution of the iceberg phenomenon in Johne’s disease through mathematical modelling”, PLOS ONE 8 (2013) e76636. https://doi.org/10.1371/journal.pone.0076636.

S. Kumar, S. Jha & S. K. Rai, “Significance of super spreader events in COVID-19”, Indian J Public Health 64 (2020) 139. https://doi.org/10.4103/ijph.IJPH_495_20.

Chief Election Officer, West Bengal, (2021). http://www.ceowestbengal. nic.in/index.

Elections in India intensified spread of COVID-19 pandemic’s second wave, 2021. https://www.straitstimes.com/asia/south-asia/ elections-in-india-intensified-spread-of-the-pandemics-second-wave.

Haridwar Kumbh Mela, 2021. https://www.haridwarkumbhmela2021. com.

India Covid: Kumbh Mela pilgrims turn into super-spreaders, 2021. https://www.bbc.com/news/world-asia-india-57005563.

State Election Commission, Uttar Pradesh, Lucknow, 2021. http://sec.up.8nic.in.

Times Now Digital (2020), timesnownews.com: https://www.timesnownews.com/delhi/article/COVID-19-delhi-hc-pullsup-aap-govt-asks-why-only-33-private-hospitals-chosen-for-reservationof-icu-beds/680984.

A. Bhuyan, “Experts criticise India’s complacency over COVID-19”, The Lancet 397 (2021) 1611. https://doi.org/10.1016/S0140-6736(21)00993-4.