The analysis of a novel COVID-19 model with the fractional-order incorporating the impact of the vaccination campaign in Nigeria via the Laplace-Adomian Decomposition Method

Authors

  • Akeem Olarewaju Yunus Department of Mathematical Sciences, Osun State University, Osogbo, Nigeria; Department of Mathematics and Statistics, Osun State College of Technology, Esa-Oke, Nigeria
  • Morufu Oyedunsi Olayiwola Department of Mathematical Sciences, Osun State University, Osogbo, Nigeria

Keywords:

Caputo fractional derivative, COVID-19 disease, Laplace-Adomian decomposition method, Vaccination rate

Abstract

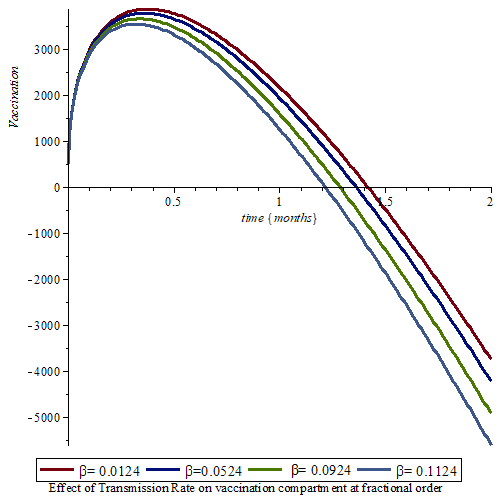
This study underscores the crucial role of COVID-19 vaccinations in managing the pandemic, with a specific focus on Nigeria. Employing a fractional-order mathematical modeling approach, the research assesses vaccination efficacy, minimum effectiveness, and duration. The model’s numerical solution is derived through the Laplace Adomian Decomposition Method (LADM), utilizing rapidly converging infinite series. Simulation results illustrate the impact of COVID-19 transmission and vaccination rates. The study concludes that implementing a vaccination strategy in an integer order proves to be the most effective approach to controlling the spread of COVID-19. These findings have significant implications for researchers, policymakers, and healthcare workers. They emphasize the central role of fractional calculus in facilitating vaccine implementation in the ongoing battle against COVID-19. The study calls for global efforts to maximize vaccination implementation for the overall benefit of public health.

Dimensions

M. Amin, M. Farman, A. Akgul & R. T. Alqahtani, “Effect of vaccination to control COVID-19 with fractal fractional operator”, Alexandria Engineering Journal 61 (2022) 3551. https://doi.org/10.1016/j.aej.2021.09.006.

T. Hussain, M. Ozair, F. Ali, S. urRehman, T. A. Assiri & E. E. Mahmoud,“ Sensitivity analysis and optimal control of COVID-19 dynamics based on SEIQR model”, Results in Physics 22 (2021) 103956. https://doi.org/10.1016/j.rinp.2021.103956.

S. Khajanchi, K. Sarkar, J. Mondal, K. S. Nisar & S. F. Abdelwahab, “Mathematical modeling of the COVID-19 pandemic with intervention strategies”, Results in Physics 25 (2021) 104285. https://doi.org/10.1016/j.rinp.2021.104285.

M. K. Kolawole, M. O. Olayiwola, A. I. Alaje, H. O. Adekunle & K. A. Odeyemi, “Conceptual analysis of the combined effects of vaccination, therapeutic actions, and human subjection to physical constraint in reducing the prevalence of COVID-19 using the homotopy perturbation method”, Beni-Suef University Journal of Basic and Applied Sciences 12 (2023) 1. https://doi.org/10.1186/s43088-023-00343-2.

K. Abbas, S. R. Procter, K. Van Zandvoort, A. Clark, S. Funk, T. Mengistu & G. Medley, “Routine childhood immunisation during the COVID-19 pandemic in Africa: a benefit-risk analysis of health benefits versus excess risk of SARS-CoV-2 infection”, The Lancet Global Health 8 (2020) 1264. https://doi.org/10.1016/S2214-109X(20)30308-9.

A. Muniyappan, B. Sundarappan, P. Manoharan, M. Hamdi, K. Raahemifar, S. Bourouis & V. Varadarajan, “Stability and numerical solutions of second wave mathematical modeling on COVID-19 and Omicron outbreak strategy of pandemic: Analytical and error analysis of approximate series solutions by using HPM”, Mathematics 10 (2022) 343. https://doi.org/10.3390/math10030343.

A. I. Alaje, M. O. Olayiwola, K. A. Adedokun, J. A. Adedeji & A. O. Oladapo, “Modified homotopy perturbation method and its application to analytical solitons of fractional-order Korteweg–de Vries equation”, Beni-Suef University Journal of Basic and Applied Sciences 11 (2022) 139. https://doi.org/10.1186/s43088-022-00317-w.

B. G. Masresha, R. Luce Jr, M. E. Shibeshi, B. Ntsama, A. N’Diaye, J. Chakauya & R. Mihigo, “The performance of routine immunization in selected African countries during the first six months of the COVID-19 pandemic”, The Pan African Medical Journal 37 (2020) https://doi.org/10.11604/pamj.supp.2020.37.1.26107.

K. A. Gaythorpe, K. Abbas, J. Huber, A. Karachaliou, N. Thakkar, K. Woodruff and M. Jit, “Impact of COVID-19-related disruptions to measles, meningococcal A and yellow fever vaccination in 10 countries”, Elife 10 (2021) 67023. https://doi.org/10.1016/j.vaccine.2022.05.074.

M. Coker, M. O. Folayan, I. C. Michelow, R. E. Oladokun, N. Torbunde & N. A. Sam-Agudu, “Things must not fall apart: the ripple effects of the COVID-19 pandemic on children in sub-Saharan Africa”, Pediatric Research 89 (2021) 1078. https://doi.org/10.1038/s41390-020-01174-y.

A. Shet, K. Carr, M. C. Danovaro-Holliday, S. V. Sodha, C. Prosperi, J. Wunderlich & A. Lindstrand, “Impact of the SARS-CoV-2 pandemic on routine immunization services: evidence of disruption and recovery from 170 countries and territories”, The Lancet Global Health 10 (2022) 186. https://doi.org/10.1016/S2214-109X(21)00512-X.

E. Leshem & A. Wilder-Smith ”COVID-19 vaccine impact in Israel and a way out of the pandemic”, The Lancet 397 (2021) 1783. https://doi.org/10.1016/S2214-109X(21)00512-X.

J. P. Figueroa, M. E. Bottazzi, P. Hotez, C. Batista, O. Ergonul, S. Gilbert & G. Kang, “Urgent needs of low-income and middle-income countries for COVID-19 vaccines and therapeutics”, The Lancet 397 (2021) 562. https://doi.org/10.17615/htxb-an45.

B. Chen, Y. Zhao, Z. Jin, D. He & H. Li, “Twice evasions of Omicron variants explain the temporal patterns in six Asian and Oceanic countries”, BMC Infectious Diseases 23 (2023) 1. https://doi.org/10.1186/s12879-023-07984-9.

S. K. Yadav, V. Kumar & Y. Akhter, “Modeling global COVID-19 dissemination data after the emergence of Omicron variant using multipronged approaches”, Current Microbiology 79 (2022) 286. https://doi.org/10.3389/fpubh.2021.783201.

O. M. Otunuga, “Analysis of multi-strain infection of vaccinated and recovered population through epidemic model: Application to COVID-19”, Plos one 17 (2022) e0271446. https://doi.org/10.1371/journal.pone.0271446.

M. Lounis, D. Bencherit, M. A. Rais & A. Riad, “COVID-19 vaccine booster hesitancy (VBH) and its drivers in Algeria: national cross-sectional survey-based study”, Vaccines 10 (2022) 621. https://doi.org/10.3390/vaccines10040621.

A. O. Yunus, M. O. Olayiwola, K. A. Adedokun, J. A. Adedeji & A. I. Alaje, “Mathematical analysis of fractional-order Caputo’s derivative of coronavirus disease model via Laplace Adomian decomposition method”, Beni-Suef University Journal of Basic and Applied Sciences 11 (2022) 144. https://doi.org/10.1186/s43088-022-00326-9.

A. Boudaoui, Y. E hadjMoussa, Z. Hammouch & S. Ullah, “A fractionalorder model describing the dynamics of the novel coronavirus (COVID-19) with nonsingular kernel”, Chaos, Solitons & Fractals 146 (2021) 110859. https://doi.org/10.1016/j.chaos.2021.110859.

A. Babaei, M. Ahmadi, H. Jafari & A. Liya, “A mathematical model to examine the effect of quarantine on the spread of coronavirus”, Chaos, Solitons & Fractals 142 (2021) 110418. https://doi.org/10.1016/j.chaos.2020.110418.

M. Arfan, M. M. Lashin, P. Sunthrayuth, K. Shah, A. Ullah, K. Iskakova & T. Abdeljawad, “On nonlinear dynamics of COVID-19 disease model corresponding to nonsingular fractional order derivative”, Medical & Biological Engineering & Computing 60 (2022) 3169. https://doi.org/10.1007/s11517-022-02661-6.

N. Debbouche, A. Ouannas, I. M. Batiha & G. Grassi, “Chaotic dynamics in a novel COVID-19 pandemic model described by commensurate and incommensurate fractional-order derivatives”, Nonlinear Dynamics 2021 (2021) 1. https://doi.org/10.1007/s11071-021-06867-5.

A. Ali, M. Y. Khan, M. Sinan, F. M. Allehiany, E. E. Mahmoud, A. H. Abdel-Aty & G. Ali, “Theoretical and numerical analysis of novel COVID-19 via fractional order mathematical model”, Results in Physics 20 (2021) 103676. https://doi.org/10.1016/j.rinp.2020.103676.

N. Faraz, Y. Khan, E. D. Goufo, A. Anjum & A. Anjum, “Dynamic analysis of the mathematical model of COVID-19 with demographic effects”, Zeitschriftf¨urNaturforschung C 75 (2020) 389. https://doi.org/10.1515/znc-2020-0121.

P. Pandey, J. F. Gomez-Aguilar, M. K. Kaabar, Z. Siri & A. M. Allah, “Mathematical modeling of COVID-19 pandemic in India using Caputo-Fabrizio fractional derivative”, Computers in biology and medicine 145 (2022) 105518. https://doi.org/10.1016/j.compbiomed.2022.105518.

M. Sivashankar, S. Sabarinathan, V. Govindan, U. Fernandez-Gamiz & S. Noeiaghdam, “Stability analysis of COVID-19 outbreak using Caputo- Fabrizio fractional differential equation”, AIMS Mathematics 8 (2023) 2720. https://doi.org/10.3934/math.2023143.

M. A. Dokuyucu & E. Celik, “Analyzing a novel coronavirus model (COVID-19) in the sense of Caputo-Fabrizio fractional operator.” Applied and Computational Mathematics, 2021 (2021) 49. https://pesquisa.bvsalud.org/global-literature-on-novel-coronavirus-2019-ncov/resource/pt/covidwho-1220284.

K. Rajagopal, N. Hasanzadeh, F. Parastesh, I. Hamarash, S. Jafari & I. Hussain, “A fractional-order model for the novel coronavirus (COVID-19) outbreak”, Nonlinear Dynamics 101 (2020) 11. https://doi.org/10.1007/s11071-020-05757-6.

K. M. Furati, I. O. Sarumi & A. Q. M. Khaliq, “Fractional model for the spread of COVID-19 subject to government intervention and public perception”, Applied mathematical modelling 95 (2021) 89. https://doi.org/10.1016/j.apm.2021.02.006.

M. A. Bahloul, A. Chahid & T. M. Laleg-Kirati, “Fractional-order SEIQRDP model for simulating the dynamics of COVID-19 epidemic”, IEEE Open Journal of Engineering in Medicine and Biology 1 (2020) 249. https://doi.org/10.1109/OJEMB.2020.3019758.

K. Kozio?, R. Stanis?awski & G. Bialic, “Fractional-order SIR epidemic model for transmission prediction of COVID-19 disease”, Applied Sciences 10 (2020) 8316. https://doi.org/10.3390/app10238316.

Z. Zhang, A. Zeb, O. F. Egbelowo & V. S. Erturk , “Dynamics of a fractional order mathematical model for COVID-19 epidemic”, Advances in Difference Equations 2020 (2020) 1. https://doi.org/10.1186/s13662-020-02873-w.

P. Verma & M. Kumar, “Analysis of a novel coronavirus (2019-nCOV) system with variable Caputo-Fabrizio fractional order”, Chaos, Solitons & Fractals 142 (2021) 110451. https://doi.org/10.1016/j.chaos.2020.110451.

S. Yadav, D. Kumar, J. Singh & D. Baleanu, “Analysis and dynamics of fractional order Covid-19 model with memory effect”, Results in Physics 24 (2021) 104017. https://doi.org/10.1016/j.chaos.2021.110859.

D. Denu & S. Kermausuor, “Analysis of a fractional-order COVID-19 epidemic model with lockdown”, Vaccines 10 (2022) 1773. https://doi.org/10.3390/vaccines10111773.

M. O. Olayiwola, A. I. Alaje & A. O. Yunus, “A Caputo fractional order financial mathematical model analyzing the impact of an adaptive minimum interest rate and maximum investment demand”, Results in Control and Optimization 2023 (2023) 100349. https://doi.org/10.1016/j.rico.2023.100349.

A. I. Alaje, M. O. Olayiwola, K. A. Adedokun, J. A. Adedeji, A. O. Oladapo & Y. O. Akeem, “The modified homotopy perturbation method and its application to the dynamics of price evolution in Caputo-fractional order Black Scholes model”, Beni-Suef University Journal of Basic and Applied Sciences 12 (2023) 93. https://doi.org/10.1186/s43088-023-00433-1.

M. O. Olayiwola, A. I. Alaje, A. Y. Olarewaju & K. A. Adedokun, “A Caputo fractional order epidemic model for evaluating the effectiveness of high-risk quarantine and vaccination strategies on the spread of COVID-19”, Healthcare Analytics 3 (2023) 100179. https://doi.org/10.1016/j.health.2023.100179.

A. O. Yunus, M. O. Olayiwola, M. A. Omoloye & A. O. Oladapo, “A fractional order model of Lassa disease using the Laplace-Adomian decomposition method”, Healthcare Analytics 2023 (2023) 100167. https://doi.org/10.1016/j.health.2023.100167.

M. O. Olayiwola & K. A. Adedokun, “A novel tuberculosis model incorporating a Caputo fractional derivative and treatment effect via the homotopy perturbation method”, Bulletin of the National Research Centre 47(2023) 121. https://doi.org/10.1016/j.health.2023.100167.

M. Ghani, I. Q. Utami, F.W. Triyayuda & M. Afifah, “A fractional SEIQR model on diphtheria disease”, Modeling Earth Systems and Environment 9 (2023) 2199. https://doi.org/10.1007/s40808-022-01615-z.

K. Issa, S. A. Olorunnisola, T. Aliu & A. A. Dauda, “Approximate solution of space fractional order diffusion equations by Gegenbauer collocation and compact finite difference scheme: Solution of space fractional diffusion equation”, Journal of the Nigerian Society of Physical Sciences 5 (2023) 1368. https://doi.org/10.46481/jnsps.2023.1368.

K. Issa, R. A. Bello & U. J. Abubakar, “Approximate analytical solution of fractional-order generalized integro-differential equations via fractional derivative of shifted Vieta-Lucas polynomial”, Journal of the Nigerian Society of Physical Sciences 6 (2024) 1821. https://doi.org/10.46481/jnsps.2024.1821.

O. Nave, U. Shemesh & I. HarTuv, “Applying Laplace Adomian decomposition method (LADM) for solving a model of Covid-19”, Computer Methods in Biomechanics and Biomedical Engineering 24 (2021) 1618. https://doi.org/10.1080/10255842.2021.1904399.

A. Ali, V. S. Erturk, A. N. W. A. R. Zeb & R. A. Khan, “Numerical solution of fractional order immunology and AIDS model via Laplace transform Adomian decomposition method”, J. Fract. Calcul. Appl. 10 (2019) 242. https://jfca.journals.ekb.eg/article308514 8f74b43e6193c678bb278bb55de3001e.pdf.

F. Haq, K. Shah, A. Khan & M. Shahzad, “Numerical solution of fractional order epidemic model of a vector-borne disease by Laplace Adomian decomposition method”, Punjab University Journal of Mathematics 49 (2020) 13. http://pu.edu.pk/images/journal/maths/PDF/Paper-2_49_2_17.pdf.

A. I. Alaje & M. O. Olayiwola, “A fractional order mathematical model for examining the spatiotemporal spread of COVID-19 in the presence of vaccine distribution”, Healthcare Analytics 4 (2023) 100230. https://doi.org/10.1016/j.health.2023.100230.

Published

2024-03-27

How to Cite

The analysis of a novel COVID-19 model with the fractional-order incorporating the impact of the vaccination campaign in Nigeria via the Laplace-Adomian Decomposition Method. (2024). Journal of the Nigerian Society of Physical Sciences, 6(2), 1830. https://doi.org/10.46481/jnsps.2024.1830

Issue

Volume 6, Issue 2, May 2024

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2024 Akeem Olarewaju Yunus, Morufu Oyedunsi Olayiwola

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

The analysis of a novel COVID-19 model with the fractional-order incorporating the impact of the vaccination campaign in Nigeria via the Laplace-Adomian Decomposition Method. (2024). Journal of the Nigerian Society of Physical Sciences, 6(2), 1830. https://doi.org/10.46481/jnsps.2024.1830