A tuberculosis model with three infected classes

Authors

  • A. O. Sangotola Department of Physical Sciences, Bells University of Technology, Ota, Nigeria
  • S. B. Adeyemo Department of Mathematics and Statistics, California State University, Long Beach, California, USA
  • O. A. Nuga Department of Physical Sciences, Bells University of Technology, Ota, Ogun State, Nigeria
  • A. E. Adeniji Department of Physical Sciences, Bells University of Technology, Ota, Ogun State, Nigeria
  • A. J. Adigun Department of Mathematical Sciences, University of Delaware, U.S.A

Keywords:

Optimal Control, Lyapunov function, Equilibrium, Basic , Jacobian

Abstract

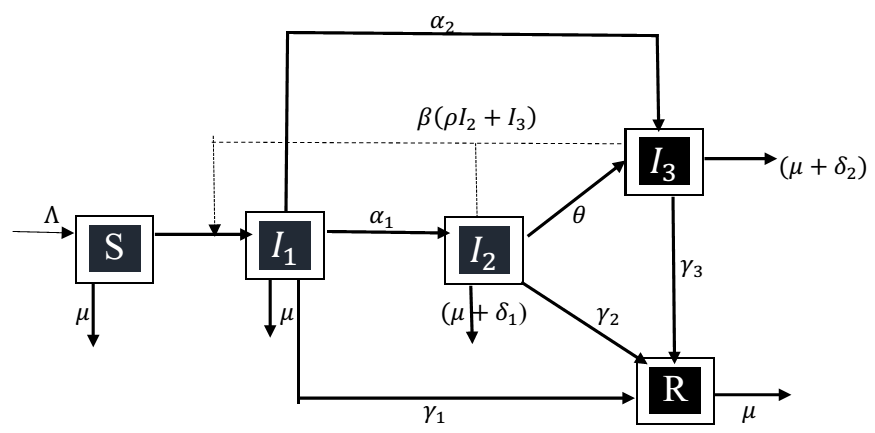
The dynamics of tuberculosis within a population cannot be adequately represented by a single infectious class. Therefore, this study develops a compartmental model encompassing latent, active, and drug-resistant populations to better capture tuberculosis dynamics in a community. Model analysis reveals that the disease-free equilibrium point is locally asymptotically stable when the basic reproduction number is below one. Moreover, the use of a suitable Lyapunov function demonstrates global asymptotic stability of the disease-free equilibrium point. An endemic equilibrium emerges when the basic reproduction number exceeds one. Sensitivity analysis is conducted for each parameter associated with the basic reproduction number, and optimal control analysis is employed to assess the impact of various control strategies on disease containment. Numerical simulations are conducted to supplement theoretical findings, illustrating the practical implications of the proposed control strategies.

Dimensions

C. C. Dim, N. R. Dim & O. Morkve, “Tuberculosis: A review of current concepts and cintrol programme in Nigeria”, Journal of Medicine 20 (2011) 191. https://www.ajol.info/index.php/njm/article/view/91573/81050.

K. K. Avilov, A. A. Romanyukha, E.M. Belilovsky & S.E. Borisov, “Mathematical modelling of the progression of active tuberculosis: Insights from fluorography data”, Infect Dis Model 7 (2022) 374. https://doi.org/10.1016/j.idm.2022.06.007.

H. Guo, M. Y. Li & Z. Shuai, “Global dynamics of a general class of multistage models for infectious diseases”, SIAM J. Appl. Math 72 (2012) 261. https://doi.org/10.1137/110827028.

D. Y. Melesse & A. B. Gumel, “Global asymptotic properties of an SEIRS model with multiple infectious stages”, J. Math. Anal. Appl. 366 (2010) 202. https://doi.org/10.1016/j.jmaa.2009.12.041.

O. M. Otunuga & M.O. Ogunsolu, “Qualitative analysis of a stochastic SEITR epidemic model with multiple stages of infection and treatment”, Infectious Disease Modelling 5 (2020) 61. https://doi.org/10.1016/j.idm.2019.12.003.

A. O. Sangotola, “A two strain mutation model with temporary and permanent recovery”, International Journal of Mathematical Sciences and Optimization: Theory and Applications 8 (2022) 37. https://doi.org/10.6084/m9.figshare.20600769.

U. M Rifanti, “Dynamic model of disease spread with two infection stages”, J. Phys.: Conf. Ser. 1567 (2020) 022075. https://doi.org/10.1088/1742-6596/1567/2/022075.

M. M. Ojo, O. J. Peter, E. F Goufo, H. S. Panigoro & F. A. Oguntolu, “Mathematical model for control of tuberculosis epidemiology”, Journal of Applied Mathematics and Computing 69 (2023) 69. htpps://doi.org/10.1007/s12190-022-01734-x.

Y. Ucakan, S. Gulen & K. Koklu, “Analysing of Tuberculosis in Turkey through SIR, SEIR and BSEIR Mathematical Models”, Mathematical and Computer Modelling of Dynamical systems 27 (2021) 179. https://doi.org/10.1080/13873954.2021.1881560.

D. K. Das, S. Khajanchi & T. K. Kar, “Transmission dynamics of tuberculosis with multiple re-infections”, Chaos Solitons and Fractals 130 (2020) 1. https://doi.org/10.1016/j.chaos.2019.109450.

F. O. Mettle, P. O. Affi & C. Twumasi, “Modelling the Transmission Dynamics of Tuberculosis in the Ashanti Region of Ghana”, Interdisciplinary Perspectives on Infectious Diseases, Hindawi Publishing Corporation 4513854 (2020) 16. https://doi.org/10.1155/2020/4513854.

D. Kereyu & S. Demie, “Transmission dynamics model of Tuberculosis with optimal control strategies in Haramaya district, Ethiopia”, Adv Differ Equ 289 (2021) 289. https://doi.org/10.1186/s13662-021-03448-z.

A. Allue-Guardia, J. I. Garcia & J. B. Torrelles, “Evolution of DrugResistant Mycobacterium tuberculosis Strains and Their Adaptation to the Human Lung Environment”, Frontiers in Microbiology 12 (2021) 1. https://doi.org/10.3389/fmicb.2021.612675.

S. Suddin, E. N. Bano & M. H. Yanni, “Mathematical Modelling of Multidrug-Resistant Tuberculosis with Vaccination”, Matematika MJIM 37 (2021) 109. https://matematika.utm.my/index.php/matematika/article/view/1318.

M. Ronoh, R. Jaroudi, P. Fotso, V. Kamdoum, N. Matendechere, J. Wairimu, R. Auma & J.A. Lugoye, “Mathematical Model of Tuberculosis with Drug Resistance Effects”, Applied Mathematics 7 (2016) 1303. https://doi.org/10.4236/am.2016.712115.

S. Adeyemo, A. Sangotola & O. Korosteleva, “Modeling Transmission Dynamics of Tuberculosis-HIV Co-Infection in South Africa”, Epidemiologia 4 (2003) 408. https://doi.org/10.3390/epidemiologia4040036.

S. Ajao, I. Olopade, T. Akinwumi, S. Adewale, & A. Adesanya, “Understanding the Transmission Dynamics and Control of HIV Infection: A Mathematical Model Approach”, Journal of the Nigerian Society of Physical Sciences 5 (2023) 1389. https://doi.org/10.46481/jnsps.2023.1389.

P. Driessche & J. Watmough, “Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission”, Math. Biosci. 180 (2002) 29. https://doi.org/10.1016/s0025-5564(02) 00108-6.

P.V. Driessche, “Reproduction numbers of infectious disease models”, Infectious Disease Modelling 2 (2017) 288. https://doi.org/10.1016/j.idm.2017.06.002.

J. LaSalle, The Stability of Dynamical Systems, Regional Conference Series in Applied Mathematics, SIAM, Philadelphia, 1976. https://epubs.siam.org/doi/pdf/10.1137/1.9781611970432.fm

W. H. Fleming & R. W. Rishel, Deterministic and Stochastic Optimal Control, Springer Science & Business Media, 2012. https://doi.org/10. 1007/978-1-4612-6380-7.

L. S. Pontryagin, V. G. Boltyanskii, R. V. Gamkrelidze, & E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Wiley, Hoboken, NJ, USA, 1962. https://doi.org/10.1002/zamm.19630431023.

Published

2024-03-06

How to Cite

A tuberculosis model with three infected classes. (2024). Journal of the Nigerian Society of Physical Sciences, 6(1), 1881. https://doi.org/10.46481/jnsps.2024.1881

Issue

Volume 6, Issue 1, February 2024

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2023 A. O. Sangotola, S. B. Adeyemo, O. A. Nuga, A. E. Adeniji, A. J. Adigun

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

A tuberculosis model with three infected classes. (2024). Journal of the Nigerian Society of Physical Sciences, 6(1), 1881. https://doi.org/10.46481/jnsps.2024.1881