Regularization Effects in Deep Learning Architecture

Abstract

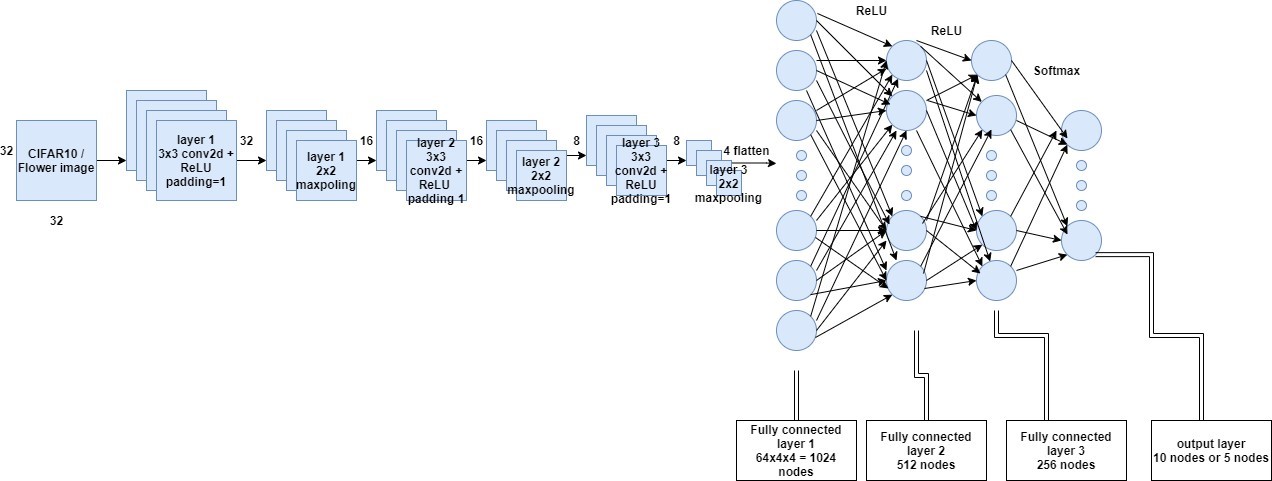
This research examines the impact of three widely utilized regularization approaches -- data augmentation, weight decay, and dropout --on mitigating overfitting, as well as various amalgamations of these methods. Employing a Convolutional Neural Network (CNN), the study assesses the performance of these strategies using two distinct datasets: a flower dataset and the CIFAR-10 dataset. The findings reveal that dropout outperforms weight decay and augmentation on both datasets. Additionally, a hybrid of dropout and augmentation surpasses other method combinations in effectiveness. Significantly, integrating weight decay with dropout and augmentation yields the best performance among all tested method blends. Analyses were conducted in relation to dataset size and convergence time (measured in epochs). Dropout consistently showed superior performance across all dataset sizes, while the combination of dropout and augmentation was the most effective across all sizes, and the triad of weight decay, dropout, and augmentation excelled over other combinations. The epoch-based analysis indicated that the effectiveness of certain techniques scaled with dataset size, with varying results.