Modelling the co-infection of malaria and zika virus disease
Keywords:
Malaria , Zika virus, Vaccination, Sterile-insect technologyAbstract
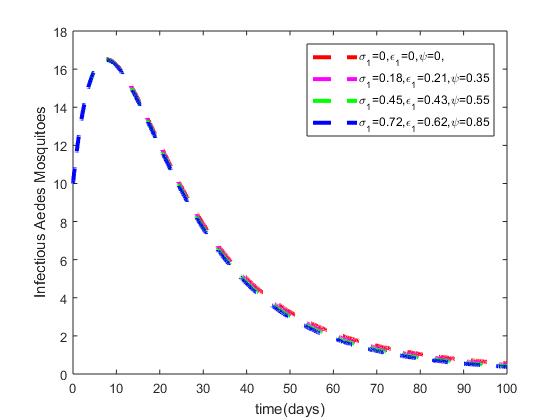
In this work, a new model for the co-infection of malaria and zika virus disease incorporating vaccination, treatment and vector control using sterile-insect technology (SIT) is formulated. The importance of this study is to highlight the possibility of the co-infection of humans with malaria and zika virus disease in any environment where both diseases co-circulate. Also, to suggest a new and comprehensive method for controlling the individual diseases and their co-infection. Through stability analysis, we showed that the disease-free equilibrium, (DFE) point of the co-infection model is locally asymptotically stable when the basic reproduction numbers, Rmz is less than one, and unstable otherwise. But, the DFE failed to be globally stable when Rmz < 1 which is an indication of existence of backward bifurcation in the model. This shows that bringing down the reproduction number, Rmz to less than one is not enough to eradicate the co-infection of the two diseases. Furthermore, it is shown that the two diseases have positive impact on the spread of each other, which could be attributed to misdiagnoses of one disease as the other. We also showed that effective treatment of infectious humans, increasing the rate of vaccination and employing sterile-insect technique to control the vectors significantly helped to control the individual diseases as well as the co-infection. From the results obtained in the study, it can be concluded that effective control of malaria and zika virus disease requires measures that will control their spread in both human and mosquito populations.
Published
How to Cite
Issue
Section
Copyright (c) 2024 Emmanuel Chidiebere Duru, Godwin Christopher Ezike Mbah, Michael Chimezie Anyanwu, Nnamani Nicholas Topman

This work is licensed under a Creative Commons Attribution 4.0 International License.






