Stagnation point flow of viscous nanofluid towards a shrinking sheet with quadratic buoyancy and thermophoresis influence: convection through porous media
Keywords:
Nonlinear convection, Nanofluid, Thermophoresis, Darcy law, Stagnation pointAbstract
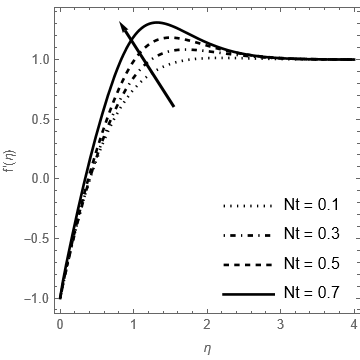
This study investigates the dynamics of heat and mass transfer, focusing on the impact of nonlinear convection and thermophoresis in the flow of viscous nanofluid towards a shrinking sheet embedded with a porous matrix. To facilitate understanding of the flow behavior, the study employs similarity variables to simplify the resulting nonlinear partial differential equations. Numerical analysis utilizing the collocation method with Legendre polynomials as basis functions reveals distinct distributions of velocity, temperature, and concentration. The results demonstrate that the dimensionless suction coefficient amplifies nanoparticle volume fraction and momentum along the stretching surface. In addition, an increase in internal frictional force leads to heightened injection of heat energy, accelerates the temperature field, and impedes nanoparticle diffusion due to heat absorption. Elevation of convection terms augments momentum, reduces energy dispersion, and enhances nanoparticle diffusion. Moreover, an increase in the dimensionless Eckert number (Ec) correlates with intensified energy and diminished diffusion concentration of the nanoparticle volume fraction.
Published
How to Cite
Issue
Section
Copyright (c) 2024 S. A. Agunbiade, J. U. Abubakar, T. L. Oyekunle, M. T. Akolade

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Similar Articles
- Ajit Kumar, Pushap Lata Sharma, Praveen Lata, Deepak Bains, Pankaj Thakur, Effect of magnetic field on the onset of thermal convection in a Jeffery nanofluid layer saturated by a porous medium: free-free, rigid-rigid and rigid-free boundary conditions , Journal of the Nigerian Society of Physical Sciences: Volume 6, Issue 2, May 2024
- Pushap Lata Sharma, Mohini Kapalta, Ashok Kumar, Deepak Bains, Sumit Gupta, Pankaj Thakur, Electrohydro dynamics convection in dielectric rotating Oldroydian nanofluid in porous medium , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 2, May 2023
- Pushap Lata Sharma, Deepak Bains, Pankaj Thakur, Thermal instability of rotating Jeffrey nanofluids in porous media with variable gravity , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 2, May 2023
- B. Laxmi, K. Chand, P. Thakur, Hydrodynamic Casson hybrid nanofluid flow across a stretching sheet in the regime of velocity slip and temperature jump,including viscous dissipation, melting, Soret and Dufour effects , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 4, November 2025
- Pushap Lata Sharma, Deepak Bains, Pankaj Thakur, Throughflow effect on bi-disperse convection in Rivlin-Ericksen fluid , Journal of the Nigerian Society of Physical Sciences: Volume 6, Issue 3, August 2024
- Anthony Anya Okeke, Nur Nadiah Abd Hamid, Wen Eng Ong, Muhammad Abbas, A numerical algorithm based on extended cubic B-spline functions for solving time-fractional convection-diffusion-reaction equation with variable coefficients , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 1, February 2025
- O. T. Wahab, I. F. Usamot, S. M. Alata, K. R. Tijani, On Nonexpansive and Expansive Semigroup of Order-Preserving Total Mappings in Waist Metric Spaces , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 1, February 2023
- Wilson Nwankwo, Kingsley Ukhurebor, Investigating the Performance of Point to Multipoint Microwave Connectivity across Undulating Landscape during Rainfall , Journal of the Nigerian Society of Physical Sciences: Volume 1, Issue 3, August 2019
- M. O. Ogunniran, A Class of Block Multi-derivative Numerical Techniques for Singular Advection Equations , Journal of the Nigerian Society of Physical Sciences: Volume 1, Issue 2, May 2019
- V. Ramanjini, G. Gopi Krishna, Mani Ramanuja, Hari Kamala Sree, S. R. Mishra, Unsteady Prandtl nanofluidic flow through stretching sheet due to mixed convection, first-order slip, and chemical reaction , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 4, November 2023
You may also start an advanced similarity search for this article.






