Assessing model selection techniques for distributions use in hydrological extremes in the presence of trimming and subsampling

Abstract

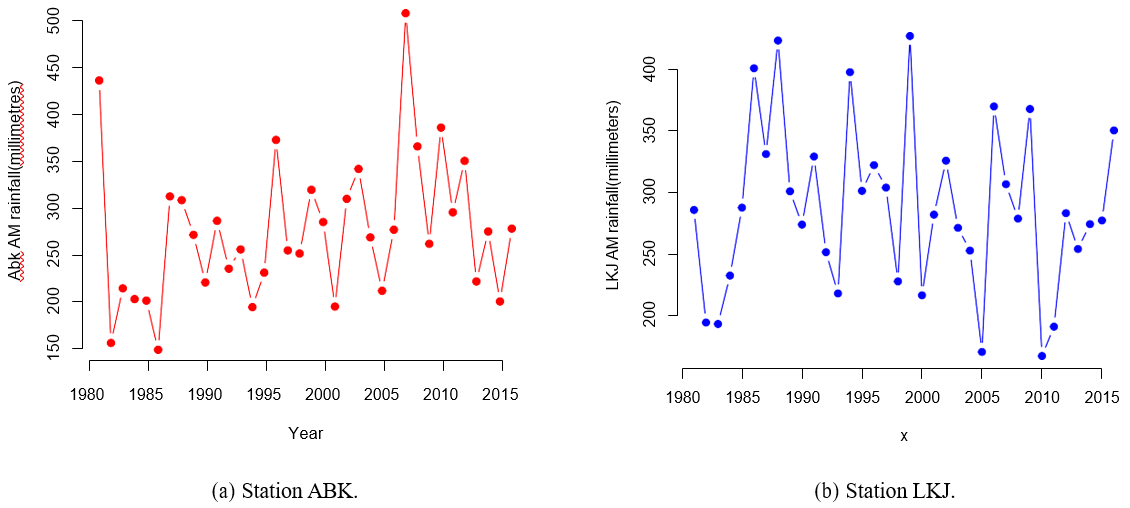
A suitable probability distribution is required to quantify and estimate hydraulic structure design for risk evaluation and management. The inability of model selection criteria to differentiate, in some cases, among candidate distributions used in the analysis of hydrological extremes is often criticised. This study verifies, with the aid of model selection techniques, the potential utility of trimming and subsampling in distinguishing between candidate distributions, which might not be feasible using the traditional goodness of fit method alone, when samples available are small. The performance of the proposed method is evaluated through its application to real and simulated yearly peak rainfall datasets. The proposed approach is then compared with several standard model selection techniques. Results show that the model selection techniques with the aid of subsampling are effective in identifying the true parent distribution for the untrimmed samples given a two-parameter distribution; contrarily, they are inefficient where a distribution with a three-parameter is the parent distribution. However, as trimming is introduced, all model selection methods recognise the true parent distribution for a three-parameter distribution. Overall, utilising trimming and subsampling with the aid of model selection methods yields promising outcomes in the analysis of hydrological extreme frequencies. Drawing from the results of numerical simulation and examination of observed data, the use of trimming and subsampling can be a viable tool in differentiating among candidate distributions used in the investigation of hydrological extreme frequencies.