Extension of hesitant fuzzy weight geometric (HFWG)-VIKOR method under hesitant fuzzy information

Abstract

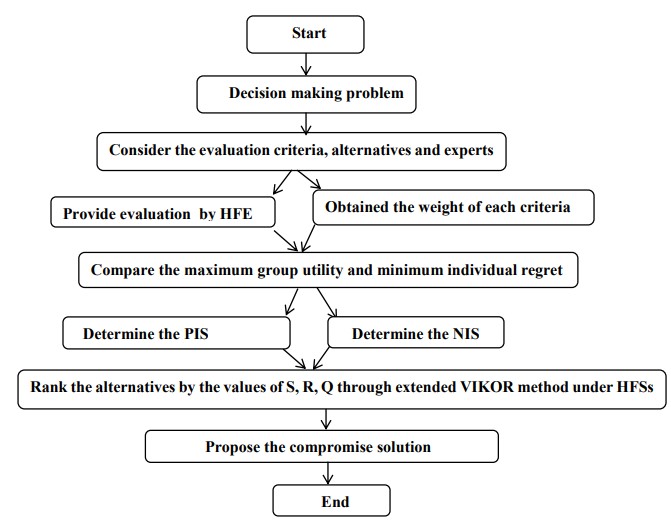
The hesitant fuzzy set (HFS) is an innovative approach to decision-making under uncertainty. This work is primarily concerned with the HFS decision matrix’s aggregated operation. The introduction of induced VIKOR procedures, various extensions of HFSs aggregation operator, and essential approaches for multi-criteria decision-making (MCDM) are presented. This technique uses the aggregation operator, the HFWG operator, to rank alternatives and identify the compromise solution closest to the ideal solution. In this research work, the hesitant fuzzy weight geometric[1]VIKOR (HFWG-VIKOR) model is a novel technique to achieve this. By combining the hesitant fuzzy elements, the HFWG aggregation operator creates aggregated values expressed as a single value. As per the scope of our research work, MCDM under hesitant fuzzy sets with the HFWG[1]VIKOR method has been used, and their result revealed the best alternative is to find out. These results indicate good potential for objectives. The multi-criteria problem is then solved using the combined HFWG-VIKOR technique, and the outcomes are presented in an easy-to-understand way owing to aggregation operators. The application of the HFWG-VIKOR technique is finally illustrated using a numerical example.