Goodness of Fit Test of an Autocorrelated Time Series Cubic Smoothing Spline Model
Keywords:
Cubic spline; goodness-of-fit test; Generalized Maximum Likelihood (GML); Generalized Cross-Validation (GCV); and Mallow CP criterion (MCP)Abstract
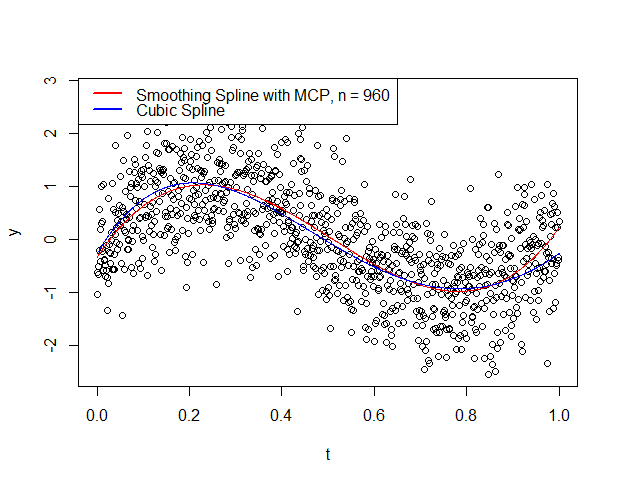
We investigated the finite properties as well as the goodness of fit test for the cubic smoothing spline selection methods like the Generalized Maximum Likelihood (GML), Generalized Cross-Validation (GCV) and Mallow CP criterion (MCP) estimators for time-series observation when there is the presence of Autocorrelation in the error term of the model. The Monte-Carlo study considered 1,000 replication with six sample sizes: 30; 60; 120; 240; 480 and 960, four degree of autocorrelations; 0.1; 0.3; 0.5; and 0.9 and three smoothing parameters; lambdaGML= 0.07271685, lambdaGCV= 0.005146929, lambdaMCP= 0.7095105. The cubic smoothing spline selection methods were also applied to a real-life dataset. The Predictive mean square error, R-square, and adjusted R-square criteria for assessing finite properties and goodness of fit among competing models discovered that the performance of the estimators is affected by changes in the sample sizes and autocorrelation levels of the simulated and real-life data set. The study concluded that the Generalized Cross-Validation estimator provides a better fit for Autocorrelated time series observation. It is recommended that the GCV works well at the four autocorrelation levels and provides the best fit for time-series observations at all sample sizes considered. This study can be applied to; non –parametric regression, non –parametric forecasting, spatial, survival and econometric observations.
Published
How to Cite
Issue
Section
Copyright (c) 2021 Journal of the Nigerian Society of Physical Sciences

This work is licensed under a Creative Commons Attribution 4.0 International License.







