Modeling the dynamics of pertussis to assess the influence of timely awareness with optimal control analysis

Authors

  • J. Andrawus
    Department of Mathematics, Federal University Dutse, 7156, Nigeria
  • J. Y. Musa
    Department of Mathematics, Federal University Dutse, 7156, Nigeria
  • S. Babuba
    Department of Mathematics, Federal University Dutse, 7156, Nigeria
  • A. Yusuf
    Department of Mathematics, Federal University Dutse, 7156, Nigeria
  • S. Qureshi
    Department of Basic Sciences and Related Studies, Mehran University of Engineering & Technology, Jamshoro – 76062, Pakistan
  • U. T. Mustapha
    Department of Mathematics, Federal University Dutse, 7156, Nigeria
  • A. Oghenefejiro
    Department of Statistics, Federal Polytechnic Orogun, Delta State, Nigeria
  • I. S. Mamba
    Department of Mathematics, Ibrahim Badamassi Babangida University Lapai, Niger State, Nigeria

Keywords:

Dynamics, Optimal control, Mathematical model, Control reproduction number, Pertussis

Abstract

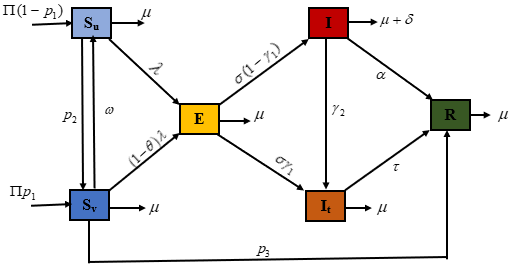
Pertussis, also known as whooping cough, is a very infectious respiratory disease that can be easily avoided with vaccination. For newborns, whooping cough poses an especially serious risk. In addition to a ”whoop”-like cough, other symptoms include sneezing, nasal congestion, and a runny nose. The bacteria that cause pertussis are called Bordetella pertussis. The upper respiratory system is the main target of the disease, and it is extremely contagious. In this work, a system of nonlinear ordinary differential equations of pertussis has been formulated to examine the impact of early treatment. Through theoretical examination, the positivity and boundlessness of the solution are confirmed. Furthermore, the local stability has been examined using the Jacobian matrix, and the equilibrium points for the system are derived for both the free and the endemic instances, and global asymptotic stability of disease-free equilibrium have been ascertained using the comparison method, which shows that the disease-free equilibrium is globally asymptotically stable if the control reproduction number is less than one. Furthermore, the global asymptotic stability of the endemic equilibrium point was determined using the Lyapunov function of the Goh-Volterra type, which shows that the endemic equilibrium point is globally asymptotically stable if the control reproduction number is greater than one. Numerical experiments are performed to validate the theoretical conclusions. The suggested model has been fitted to real Austrian pertussis data, demonstrating that it is appropriate for the data. The control reproduction number was also used to test the sensitivity analysis of all of the parameters of the proposed model. The results indicate that the effective contact rate is the parameter that is more sensitive to increasing the control reproduction number. In contrast, the awareness rate is the parameter that is most sensitive to decreasing the number of control reproductions, and optimal control analysis has also been performed in this work. Numerical simulation reveals that awareness is the most influential parameter in reducing infection in the population. Moreover, vaccination and treatment are also very important in controlling pertussis in society.

Dimensions

[1] B. Surmann, J. Witte, M. Batram, C. P. Criee, C. Hermann, A. Leischker, J. Schelling, M. Steinm¨uller, K. Wahle, A. F. Heiseke & P. Marijic, “Epidemiology of Pertussis and Pertussis-Related Complications in Adults: A German Claims Data”, Infectious Diseases and Therapy 13 (2024) 385. https://doi.org/10.1007/s40121-023-00912-z. DOI: https://doi.org/10.1007/s40121-023-00912-z

[2] M. Korppi, “Coqueluche: ainda um desafio”, Jornal de Pediatria 89 (2013) 520. https://doi.org/10.1016/j.jped.2013.09.001. DOI: https://doi.org/10.1016/j.jped.2013.09.001

[3] P. Pesco, P. Bergero, G. Fabricius, & D. Hozbor, “Modelling the effect of changes in vaccine effectiveness and transmission contact rates on pertussis epidemiology”, Epidemics 7 (2014) 13. https://doi.org/10.1016/j.epidem.2014.04.001. DOI: https://doi.org/10.1016/j.epidem.2014.04.001

[4] M. Suleman & S. Riaz, “An optimal control of vaccination applied to whooping cough model”, Punjab University Journal of Mathematics 51 (2020) 121. https://pu.edu.pk/images/journal/maths/PDF/Paper-9_515_2019.pdf.

[5] M. M. Alqarni, A. Nasir, M. A. Alyami, A. Raza, J. Awrejcewicz, M. Rafiq, N. Ahmed, T. Sumbal Shaikh & E. E. Mahmoud, “A SEIR Epidemic Model of Whooping Cough-Like Infections and Its Dynamically Consistent Approximation”, Complexity 2022 (2022) 3642444. https://doi.org/10.1155/2022/3642444. DOI: https://doi.org/10.1155/2022/3642444

[6] Immunization, Vaccines and Biologicals, by World Health Organization, (2024). https://www.who.int/teams/immunization-vaccines-and-biologicals.

[7] A. I. K. Butt, “Atangana-Baleanu fractional dynamics of predictive whooping cough model with optimal control analysis”, Symmetry 15 (2023) 1773. https://doi.org/10.3390/sym15091773. DOI: https://doi.org/10.3390/sym15091773

[8] Y. H. Choi, H. Campbell, G. Amirthalingam, A. J. Van Hoek & E. Miller, “Investigating the pertussis resurgence in England and Wales, and options for future control”, BMC Medicine 14 (2016) 1. https://doi.org/10.1186/s12916-016-0665-8. DOI: https://doi.org/10.1186/s12916-016-0665-8

[9] National Centre for Immunization and Respiratory Diseases, by Centre for Disease Control and Prevention, (2024). https://www.cdc.gov/ncird/index.html.

[10] Immunization program data: regional and country, by World Health Organization, (2022). https://www.who.int/publications/i/item/9789290619802.

[11] Nigeria Centre for Disease Control and Prevention (2011). https://ncdc.gov.ng/.

[12] A. C. Freitas, V. Okano & J. C. R. Pereira, “Pertussis booster vaccine for adolescents and young adults in S˜ao Paulo, Brazil”, Revista de Saude Publica 45 (2011) 1162. https://doi.org/10.1590/s0034-89102011000600008. DOI: https://doi.org/10.1590/S0034-89102011000600008

[13] D. Jayasundara, E. Lee, S. Octavia, R. Lan, M. M. Tanaka, & J. G. Wood, “Emergence of pertactin-deficient pertussis strains in Australia can be explained by models of vaccine escape”, Epidemics 31 (2020) 100388. https://doi.org/10.1016/j.epidem.2020.100388. DOI: https://doi.org/10.1016/j.epidem.2020.100388

[14] A. A. Yakubu, F. A. Abdullah, A. I. M. Ismail & Y. M. Yatim, “Global stability analysis of pertussis transmission dynamics with maternally derivedimmunity compartment”, AIP Conference Proceedings 2423 (2021). https://doi.org/10.1063/5.0073271. DOI: https://doi.org/10.1063/5.0075562

[15] E. Yaylali, J. S. Ivy, R. Uzsoy, E. Samoff, A. M. Meyer & J. M. Maillard, “Modeling the effect of public health resources and alerting on the dynamics of pertussis spread”, Health Systems 5 (2016) 81. https://doi.org/10.1057/hs.2015.6. DOI: https://doi.org/10.1057/hs.2015.6

[16] P. Misra & D. K. Mishra, “Modelling the effect of booster vaccination on the transmission dynamics of diseases that spread by droplet infection”, Nonlinear Analysis: Hybrid Systems 3 (2009) 657. https://doi.org/10.1016/j.nahs.2008.10.002. DOI: https://doi.org/10.1016/j.nahs.2009.06.001

[17] M. van Boven, H. E. de Melker, J. F. Schellekens, & M. Kretzschmar, “Waning immunity and sub-clinical infection in an epidemic model: implications for pertussis in The Netherlands”, Mathematical Biosciences 164 (2000) 161. https://doi.org/10.1016/s0025-5564(00)00009-2. DOI: https://doi.org/10.1016/S0025-5564(00)00009-2

[18] L. Mamadou Diagne, F. B. Agusto, H. Rwezaura, J. M. Tchuenche & S. Lenhart, “Optimal control of an epidemic model with treatment in the presence of media coverage”, Scientific African 24 (2024) e02138. https://doi.org/10.1016/j.sciaf.2024.e02138. DOI: https://doi.org/10.1016/j.sciaf.2024.e02138

[19] A. Stuart & A. R. Humphries, Dynamical Systems and Numerical Analysis, Vol. 2, Cambridge University Press, Cambridge, UK, 1998. https://assets.cambridge.org/97805214/96728/frontmatter/9780521496728 frontmatter.pdf.

[20] U. T. Mustapha, A. Ado, A. Yusuf, S. Qureshi & S. S. Musa, “Mathematical dynamics for HIV infections with public awareness and viral load detectability”, Mathematical Modelling and Numerical Simulation with Applications, 3 (2023) 256. https://doi.org/10.53391/mmnsa.1349472. DOI: https://doi.org/10.53391/mmnsa.1349472

[21] G. Djatcha Yaleu, S. Bowong, E. Houpa Danga & J. Kurths, “Mathematical analysis of the dynamical transmission of Neisseria meningitidis serogroup A”, International Journal of Computer Mathematics 94 (2017) 2409. http://dx.doi.org/10.1080/00207160.2017.1283411. DOI: https://doi.org/10.1080/00207160.2017.1283411

[22] P. Van De Driessche & J. Watmough, “Reproduction number and sub-threshold endemic equilibrium for compartmental models of disease transmission”, Mathematical Biosciences 180 (2002) 29. https://doi.org/10.1016/s0025-5564(02)00108-6. DOI: https://doi.org/10.1016/S0025-5564(02)00108-6

[23] Y. U. Ahmad, J. Andrawus, A. Ado, Y. A. Maigoro, A. Yusuf, S. Althobaiti & U. T. Mustapha, “Mathematical modeling and analysis of human-to-human monkeypox virus transmission with post-exposure vaccination”, Modeling Earth Systems and Environment 10 (2024) 2711. https://doi.org/10.1007/s40808-023-01920-1. DOI: https://doi.org/10.1007/s40808-023-01920-1

[24] J. Andrawus, A. Yusuf, U. T. Mustapha, A. S. Alshom-rani & D. Baleanu, “Unravelling the dynamics of Ebola virus with contact tracing as control strategy”, Fractals, 31 (2023) 2340159. https://doi.org/10.1142/S0218348X2340159X. DOI: https://doi.org/10.1142/S0218348X2340159X

[25] J. Andrawus, A. I. Muhammad, B. A. Denue, A. Yusuf & S. Salahshour, “Unraveling the importance of early awareness strategy on the dynamics of drug addiction using mathematical modeling approach”, Chaos: An Interdisciplinary Journal of Nonlinear Science, 34 (2024). https://doi.org/10.1063/5.0203892. DOI: https://doi.org/10.1063/5.0203892

[26] O. Johnson & H. O. S. Edogbanya, “Mathematical modeling for mitigating pertussis resurgence in the post-COVID-19 era: A sensitivity analysis and intervention strategies”, International Journal of Novel Research in Physics Chemistry & Mathematics 11 (2024) 12. https://doi.org/10.5281/zenodo.10721146.

[27] Annual Epidemiological Report pertussis, by European Center of Disease Control, (2022). https://www.ecdc.europa.eu/sites/default/files/documents/PERT_AER_2022_Report.pd.

[28] J. P. Lasalle, The stability of dynamical systems, Regional conference series in applied mathematics, SIAM, Philadelphia, 1976. https://epubs.siam.org/doi/pdf/10.1137/1.9781611970432.bm.

[29] R. Craig, E. Kunkel, N. S. Crowcroft, M. C. Fitzpatrick, H. De Melker, B. M. Althouse & S. Bolotin, “Asymptomatic infection and transmission of pertussis in households: A systematic review”, Clinical Infectious Diseases 70 (2020) 152. https://doi.org/10.1093/cid/ciz531. DOI: https://doi.org/10.1093/cid/ciz531

[30] P. M. Luz, C. T. Codec¸o, G. L. Werneck & C. J. Struchiner, “A modelling analysis of pertussis transmission and vaccination in Rio de Janeiro, Brazil”, Epidemiology, 134 (2006) 850. https://doi.org/10.1017/S095026880500539X. DOI: https://doi.org/10.1017/S095026880500539X

[31] U. T. Mustapha, A. I. Muhammad, A. Yusuf, N. Althobaiti, A. I. Aliyu & J. Andrawus, “Mathematical dynamics of meningococcal meningitis: Examining carrier diagnosis and prophylaxis treatment”, International Journal of Applied and Computational Mathematics 11 (2025) 77. https://doi.org/10.1007/s40819-025-01890-1. DOI: https://doi.org/10.1007/s40819-025-01890-1

[32] K. G. Ibrahim, J. Andrawus, A. Abubakar, A. Yusuf, S. I. Maiwa, K. Bitrus, M. Sani, I. Abdullahi, S. Babuba & J. Jonathan, “Mathematical analysis of chickenpox population dynamics unveiling the impact of booster in enhancing recovery of infected individuals”, Modeling Earth Systems and Environment 11 (2025) 1. https://doi.org/10.1007/s40808-024-02219-5. DOI: https://doi.org/10.1007/s40808-024-02219-5

[33] J. Andrawus, A. Abubakar, A. Yusuf, A. A. Andrew, B. Uzun & S. Salahshour, “Impact of public awareness on haemo-lyphatic and meningo-encepphalitic stage of sleeping sickness using mathematical model approach”, European Physical Journal Special Topics (2024) 1.

https://doi.org/10.1140/epjs/s11734-024-01417-7. DOI: https://doi.org/10.1140/epjs/s11734-024-01417-7

[34] J. Andrawus, Y. U. Ahmad, A. A. Andrew, A. Yususf, S. Qureshe, B. Akawu, H. Abdul & S. Salahshour, “Impact of surveillance in human-to-human transmission of monkeypox virus”, The European Physical Journal Special Topics (2024) 1. https://doi.org/10.1140/epjs/s11734-024-01346-5. DOI: https://doi.org/10.1140/epjs/s11734-024-01346-5

[35] B. Heimann, W. H. Fleming & R. W. Rishel, “Deterministic and stochastic optimal control”, Zeitschrift f”ur Angewandte Mathematik und Mechanik 59 (1979) 494. https://doi.org/10.1002/zamm.19790590940. DOI: https://doi.org/10.1002/zamm.19790590940

[36] J. Andrawus, S. Abdulrahman, R. V. K. Singh & S. S. Manga, “Optimal control of mathematical modelling for Ebola virus population dynamics in the presence of vaccination”, DUJOPAS 8 (2022) 126. https://doi.org/10.4314/dujopas.v8i1b.15. DOI: https://doi.org/10.4314/dujopas.v8i1b.15

Model (2) diagrammatical description.

Published

2025-08-18

How to Cite

Modeling the dynamics of pertussis to assess the influence of timely awareness with optimal control analysis. (2025). Journal of the Nigerian Society of Physical Sciences, 7(4), 2732. https://doi.org/10.46481/jnsps.2025.2732

Issue

Volume 7, Issue 4, November 2025 (In Progress)

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2025 J. Andrawus, J. Y. Musa, S. Babuba, A. Yusuf, S. Qureshi, U. T. Mustapha, A. Oghenefejiro, I. S. Mamba (Author)

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Modeling the dynamics of pertussis to assess the influence of timely awareness with optimal control analysis. (2025). Journal of the Nigerian Society of Physical Sciences, 7(4), 2732. https://doi.org/10.46481/jnsps.2025.2732