Eigensolutions and thermodynamic properties constrained by magnetic field of cyclotron frequency

Authors

  • C. A. Onate
    Department of Physics, Bowen University, Iwo, Nigeria
  • S. O. Mobolaji
    Department of Physics, Bowen University, Iwo, Nigeria
  • J. A. Akinpelu
    Department of Physics, Bowen University, Iwo, Nigeria

Keywords:

Bound state, Eigensolution, Thermal properties, Partition function, Potential model

Abstract

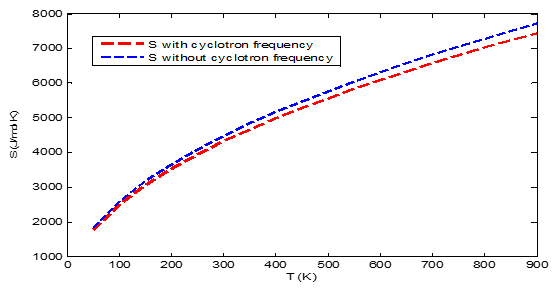
The present work investigates the influence of cyclotron frequency on the energy spectrum and thermodynamic properties of a quantum system. The energy as a function of the quantum number unveils an increase in the system's energy due to the presence of cyclotron frequency, making it open-ended by curtailing its negativity. The screening parameter significantly shapes the system’s energy, increasing at the initial point due to Landau quantization and then monotonically decreasing as a result of weakness of Coulomb interaction. The study also revealed that the parameter a and b impacted the energy differently as the cyclotron frequency altering the system’s confinement behaviours. Similarly, the partition function (Z) and some thermodynamic properties (TP), are analyzed under varying temperatures and parameter conditions. The presence of the cyclotron frequency (CF) reduces the Z and the TP due to Zeeman effect. The TP (H and S) exhibited similar characteristics. Thus, the presence of CF affects the stability of the system. This study finds applications in quantum wells and dots, fusion energy, magnetic quantum computing, and quantum statistical mechanics.

Dimensions

[1] C. O. Edet, U. S. Okorie, G. Osobonye, A. N. Ikot, G. J. Rampho & R. Sever, “Thermal properties of Deng-Fan-Eckart potential model using Poisson summation approach”, J. Math. Chem. 58 (2020) 989. https://doi.org/10.1007/s10910-020-01107-4. DOI: https://doi.org/10.1007/s10910-020-01107-4

[2] I. B. Okon, O. O. Popoola, E. Omugbe, A. D. Antia, C. N. Isonguyo & E. E. Ituen, “Thermodynamic properties and bound state solutions of Schrödinger equation with Möbius square plus screened-Kratzer potential using Nikiforov-Uvarov method”, Comp. Theor. Chem. 1196 (2021) 113132. https://doi.org/10.1016/j.comptc.2020.113132. DOI: https://doi.org/10.1016/j.comptc.2020.113132

[3] A. N. Ikot, U. S. Okorie, R. Sever & G. J. Rampho, “Eigensolution, expectation values and thermodynamic properties of the screened Kratzer potential”, Eur. Phys. J. Plus 134 (2019) 386. https://doi.org/10.1140/epjp/i2019-12783-x. DOI: https://doi.org/10.1140/epjp/i2019-12783-x

[4] G. J. Rampho, A. N. Ikot, C. O. Edet & U. S. Okorie, “Energy spectra and thermal properties of diatomic molecules in the presence of magnetic and AB fields with improved Kratzer potential”, Mol. Phys. 119 (2021) e1821922. https://doi.org/10.1080/00268976.2020.1821922. DOI: https://doi.org/10.1080/00268976.2020.1821922

[5] K. O. Emeje, C. A. Onate, I. B. Okon, E. Omugbe, E. S. Eyube, D. B. Olanrewaju & E. Aghemenloh, “Eigensolution and thermodynamic properties of standard Coulombic potential”, J. Low Temp. Phys. 215 (2024) 109. https://doi.org/10.1007/s10909-024-03074-5. DOI: https://doi.org/10.1007/s10909-024-03074-5

[6] Y. Jiang, L. Liu, J. Yan & Z. Wu, “Room-to-low temperature thermo-mechanical behavior and corresponding constitutive model of liquid oxygen compatible epoxy composites”, Comp. Sci. Techn. 245 (2024) 110357. https://doi.org/10.1016/j.compscitech.2023.110357. DOI: https://doi.org/10.1016/j.compscitech.2023.110357

[7] M. Habibinejad, R. Khordad & A. Ghanbari, “Specific heat at constant pressure, enthalpy and Gibbs free energy of boron nitride (BN) using q-deformed exponential-type potential”, Physica B 613 (2021) 412940. https://doi.org/10.1016/j.physb.2021.412940. DOI: https://doi.org/10.1016/j.physb.2021.412940

[8] R. Khordad & A. Ghanbari, “Theoretical prediction of thermal properties of K2 diatomic molecule using generalized Möbius square potential”, Int. J. Thermophys. 42 (2021) 115. https://doi.org/10.1007/s10765-021-02865-2. DOI: https://doi.org/10.1007/s10765-021-02865-2

[9] C. A. Onate, I. B. Okon, E. Omugbe, E. S. Eyube, B. A. Al-Asbahi, Y. A. Kumar, K. O. Emeje, E. Aghemenloh, A. R. Obasuyi, V. O. Obaje & T. O. Etchie, “Theoretical prediction of molar entropy of modified shifted Morse potential for gaseous molecules”, Chem. Phys. 582 (2024) 112294. https://doi.org/10.1016/j.chemphys.2024.112294. DOI: https://doi.org/10.1016/j.chemphys.2024.112294

[10] E. S. Eyube, P. P. Notani & H. Samaila, “Analytical prediction of enthalpy and Gibbs free energy of gaseous molecules”, Chem. Thermody. Thermal Analysis 6 (2022) 100060. https://doi.org/10.1016/j.ctta.2022.100060. DOI: https://doi.org/10.1016/j.ctta.2022.100060

[11] K. O. Emeje, E. Aghemenloh & C. A. Onate, “Analytical determination of enthalpy, heat capacity and Gibbs free energy for nitrogen and iodine”, Chem. Phys. Lett. 844 (2024) 141271. https://doi.org/10.1016/j.cplett.2024.141271. DOI: https://doi.org/10.1016/j.cplett.2024.141271

[12] W. Song, N. Martsinovich, W. M. Heckl & M. Lackinger, “Thermodynamic of halogen bonded monolayer self-assembly at the liquid-solid interface”, Chem. Commun. 50 (2014) 13465. https://doi.org/10.1039/C4CC06251E. DOI: https://doi.org/10.1039/C4CC06251E

[13] K. I. Amano, T. Yoshidome, Y. Harano, K. Oda & M. Kinoshita, “Theoretical analysis on thermal stability of a protein focused on the water entropy”, Chem. Phys. Lett. 474 (2009) 190. https://doi.org/10.1016/j.cplett.2009.04.025. DOI: https://doi.org/10.1016/j.cplett.2009.04.025

[14] N. M. Yunus, M. I. A. Mutalib, Z. Man, M. A. Bustam & T. Murugesan, “Solubility of CO2 in pyridinium based ionic liquids”, Chem. Engr. J. 94 (2012) 189. https://doi.org/10.1016/j.cej.2012.02.033. DOI: https://doi.org/10.1016/j.cej.2012.02.033

[15] N. P. Stadie, M. Murialdo, C. C. Ahn & B. Fultz, “Anomalous isosteric enthalpy of adsorption of methane on zeolite-templated carbon supporting information”, J. Am. Chem. Soc. 135 (2013) 990. https://doi.org/10.1021/ja311415m. DOI: https://doi.org/10.1021/ja311415m

[16] T. Zhang, G. S. Ellis, S. C. Ruppel, K. Milliken & R. Yang, “Effect of organic-matter type and thermal maturity on methane adsorption in shale-gas systems”, Org. Geochem 47 (2012) 120. https://doi.org/10.1016/j.orggeochem.2012.03.012. DOI: https://doi.org/10.1016/j.orggeochem.2012.03.012

[17] S. A. Moses, J. P. Covey, M. T. Miecnikowski, B. Yan, B. Gadway, J. Ye & D. S. Jin, “Creation of a low entropy quantum gas of polar molecules in an optical lattice”, Science 350 (2015) 659. https://doi.org/10.1126/science.aac640. DOI: https://doi.org/10.1126/science.aac6400

[18] S. Dastidar, C. J. Hawley, A. D. Dillon, A. D. Gutierrez-Perez, J. E. Spanier & A. T. Fafarman, “Quantitative phase-change thermodynamics and metastability of perovskite-phase cesium lead iodide”, J. Phys. Chem. Lett. 8 (2017) 1278. https://doi.org/10.1021/acs.jpclett.7b00134. DOI: https://doi.org/10.1021/acs.jpclett.7b00134

[19] C. Tezcan & R. Sever, “A general approach for the exact solution of the Schrödinger equation”, Int. J. Theor. Phys. 48 (2009) 337. https://doi.org/10.1007/s10773-008-9806-y. DOI: https://doi.org/10.1007/s10773-008-9806-y

[20] R. L. Greene & C. Aldrich, “Variational wave functions for screened Coulomb potential”, Phys. Rev. A 14 (1976) 2363. https://doi.org/10.1103/PhysRevA.14.2363. DOI: https://doi.org/10.1103/PhysRevA.14.2363

[21] C. A. Onate, J. A. Akinpelu, O. O. Ajani, B. B. Deji-Jinadu, F. O. Aweda, J. B. Fashae & O. O. Jegede, “Molar enthalpy and heat capacity for symmetric trigonometric Rosen-Morse plus Pöschl-Teller potential”, South Afr. J. Chem. Eng. 51 (2025) 15. https://doi.org/10.1016/j.sajce.2024.10.007. DOI: https://doi.org/10.1016/j.sajce.2024.10.007

[22] S. H. Dong, R. Lemus & A. Frank, “Ladder operators for the Morse potential”, Int. J. Quant. Chem. 86 (2002) 433. https://doi.org/10.1002/qua.10038. DOI: https://doi.org/10.1002/qua.10038

[23] R. Khordad & H. R. Sedehi, “Thermodynamic properties of a double ring-shaped quantum dot at low and high temperatures”, J. Low Temp. Phys. 190 (2018) 200. https://doi.org/10.1007/s10909-017-1831-x. DOI: https://doi.org/10.1007/s10909-017-1831-x

[24] S. H. Dong, “The SU(2) realization for the Morse potential and its coherent states”, Can. J. Phys. 80 (2002) 129. https://doi.org/10.1139/p01-130. DOI: https://doi.org/10.1139/p01-130

[25] G. H. Liu, Q. C. Ding, C. W. Wang & C. S. Jia, “Unified non-fitting explicit formulation of thermodynamic properties for five compounds”, J. Mol. Str. 1294 (2023) 136543. https://doi.org/10.1016/j.molstruc.2023.136543. DOI: https://doi.org/10.1016/j.molstruc.2023.136543

[26] S. H. Dong & M. Cruz-Irisson, “Energy spectrum for a modified Rosen-Morse potential solved by proper quantization rule and its thermodynamic properties”, J. Math. Chem. 50 (2012) 881. https://doi.org/10.1007/s10910-011-9931-3. DOI: https://doi.org/10.1007/s10910-011-9931-3

[27] R. Khordad & A. Ghanbari, “Theoretical prediction of thermodynamic functions of TiC: Morse ring-shaped potential”, J. Low Temp. Phys. 199 (2020) 1198. https://doi.org/10.1007/s10909-020-02368-8. DOI: https://doi.org/10.1007/s10909-020-02368-8

[28] R. Khordad & A. Ghanbari, “Analytical calculations of thermodynamic functions of lithium dimer using modified Tietz and Badawi-Bessis-Bessis potentials”, Comput. Theor. Chem. 1155 (2019) 1. https://doi.org/10.1016/j.comptc.2019.03.019. DOI: https://doi.org/10.1016/j.comptc.2019.03.019

[29] S. H. Dong, M. Lozada-Cassou, J. Yu, F. Jimenez-Ángeles & A. L. Rivera, “Hidden symmetries and thermodynamic properties for a harmonic oscillator plus an inverse square potential”, Int. J. Quant. Chem. 107 (2007) 366. https://doi.org/10.1002/qua.21103. DOI: https://doi.org/10.1002/qua.21103

[30] M. L. Strekalov, “An accurate closed-form expression for the partition function of Morse oscillators”, Chem. Phys. Lett. 439 (2007) 209. https://doi.org/10.1016/j.cplett.2007.03.052. DOI: https://doi.org/10.1016/j.cplett.2007.03.052

[31] C. S. Jia, R. Zeng, X. L. Peng, L. H. Zhang & Y. L. Zhao, “Entropy of gaseous phosphorus dimer”, Chem. Eng. Sci. 190 (2018) 122. https://doi.org/10.1016/j.ces.2018.06.009. DOI: https://doi.org/10.1016/j.ces.2018.06.009

[32] X. L. Peng, R. Jiang, C. S. Jia, L. H. Zhang & Y. L. Zhao, “Gibbs free energy of gaseous phosphorus dimer”, Chem. Eng. Sci. 190 (2018) 122. https://doi.org/10.1016/j.ces.2018.06.027. DOI: https://doi.org/10.1016/j.ces.2018.06.027

[33] C. S. Jia, C. W. Wang, L. H. Zhang, X. L. Peng, H. M. Tang, J. Y. Liu, Y. Xiong & R. Zeng, “Predictions of entropy for diatomic molecules and gaseous substances”, Chem. Phys. Lett. 692 (2018) 57. https://doi.org/10.1016/j.cplett.2017.12.013. DOI: https://doi.org/10.1016/j.cplett.2017.12.013

[34] R. Jiang, C. S. Jia, Y. Q. Wang, X. L. Peng & L. H. Zhang, “Prediction of Gibbs free energy for the gases Cl2, Br2, and HCl”, Chem. Phys. Lett. 726 (2019) 83. https://doi.org/10.1016/j.cplett.2019.04.040. DOI: https://doi.org/10.1016/j.cplett.2019.04.040

[35] C. S. Jia, J. Li, Y. S. Liu, X. L. Peng, X. Jia, L. H. Zhang, R. Jiang, X. P. Li, J. Y. Liu & Y. L. Zhao, “Predictions of thermodynamic properties for hydrogen sulfide”, J. Mol. Liquid 315 (2020) 113751. https://doi.org/10.1016/j.molliq.2020.113751. DOI: https://doi.org/10.1016/j.molliq.2020.113751

[36] M. H. Abdulameer, A. B. M. Ali, A. K. Nemah, P. Kanjariya, A. Rajiv, M. Agarwal, P. Kaur & A. A. Almehizia, “Prediction of molar entropy of gaseous molecules for a new Pöschl-Teller potential model”, Int. J. Quant. Chem. 124 (2024) e27505. https://doi.org/10.1002/qua.27505. DOI: https://doi.org/10.1002/qua.27505

Published

2025-08-25

How to Cite

Eigensolutions and thermodynamic properties constrained by magnetic field of cyclotron frequency. (2025). Journal of the Nigerian Society of Physical Sciences, 7(4), 2869. https://doi.org/10.46481/jnsps.2025.2869

Issue

Volume 7, Issue 4, November 2025

Section

Physics & Astronomy
Copyright & Licensing

Copyright (c) 2025 C. A. Onate, S. O. Mobolaji, J. A. Akinpelu (Author)

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Eigensolutions and thermodynamic properties constrained by magnetic field of cyclotron frequency. (2025). Journal of the Nigerian Society of Physical Sciences, 7(4), 2869. https://doi.org/10.46481/jnsps.2025.2869