Optimizing initial chlorine dosage at an injection point along a water distribution pipe
Keywords:
Optimizing, Chlorine dosage, Chlorine residual, Water distribution pipeAbstract
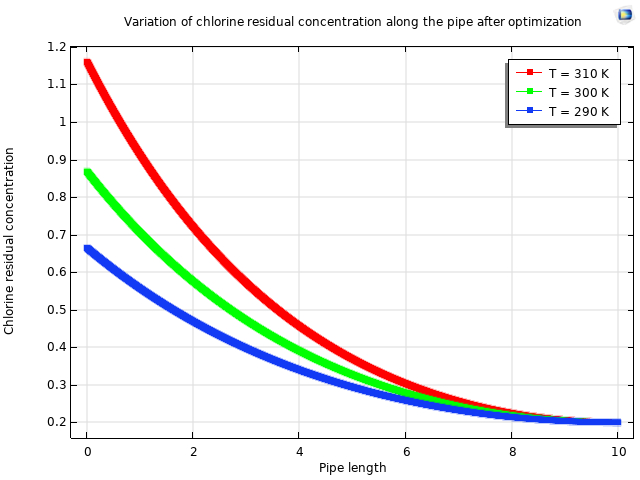
This study proposed a gradient-based optimization framework for determining the optimal initial chlorine dosage at an injection point along a water distribution pipe, with the aim of ensuring microbial safety and regulatory compliance while minimizing chlorine overuse and associated costs. Leveraging the SNOPT (Sparse Nonlinear Optimizer) algorithm integrated within the COMSOL Multiphysics environment, the approach systematically refined dosing strategies based on temperature-dependent chlorine decay dynamics. Prior to optimization, a uniform dosage of 1 mg/L yielded suboptimal outlet residuals; 0.30 mg/L, 0.23 mg/L, and 0.17 mg/L at 290K, 300K, and 310K, respectively. Post-optimization, precise dosing of 0.66 mg/L, 0.87 mg/L, and 1.16 mg/L achieved the target residual concentration of 0.2 mg/L across the same temperature conditions, enhancing disinfection control by 13-17%. The results demonstrate that this method delivers accurate, adaptive chlorine dosing, reducing the risk of harmful disinfection byproducts (DBPs), improving cost efficiency, and supporting sustainable water quality management. The proposed model is suitable for real-time integration into supervisory control systems, offering a practical pathway for advancing water safety, operational effectiveness, and environmental stewardship.
Published
How to Cite
Issue
Section
Copyright (c) 2025 John Tulirinya, Mathew Kinyanju, Samuel Mutua, Asaph Muhumuza (Author)

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Similar Articles
- A. M. Asere, T. O. Owolabi, B. D. Alafe, O. P. Alabi, M. B. Alimi, Assessment of Excess Gamma Dose Exposure Level in Typical Nigeria Commercial Building Materials Distribution Outlets , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 3, August 2021
- J. O. Coker, H. H. Akpan, A. O. Atilade, O. F. Ojo, Seasonal Comparison of Potential Groundwater Aquifer in Ijebu-Ife, South-West, Nigeria, using Dipole-Dipole Array and Electromagnetic Methods , Journal of the Nigerian Society of Physical Sciences: Volume 2, Issue 4, November 2020
- Raja Aqib Shamim, Majid Khan Majahar Ali, Optimizing discrete dutch auctions with time considerations: a strategic approach for lognormal valuation distributions , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 1, February 2025
- K. O. Sodeinde, S. O. Olusanya, D. U. Momodu, V. F. Enogheghase, O. S. Lawal, Waste glass: An excellent adsorbent for crystal violet dye, Pb2+ and Cd2+ heavy metals ions decontamination from wastewater , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 4, November 2021
- R. El chaal, M. O. Aboutafail, Statistical Modelling by Topological Maps of Kohonen for Classification of the Physicochemical Quality of Surface Waters of the Inaouen Watershed Under Matlab , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 2, May 2022
- P. K. Alimo, G. Lartey-Young, S. Agyeman, T. Y. Akintunde, E. Kyere-Gyeabour, F. Krampah, A. Awomuti, O. Oderinde, A. O. Agbeja, O. G. Afolabi, Spatial distribution and policy implications of the exhaust emissions of two-stroke motorcycle taxis: a case study of southwestern state in Nigeria , Journal of the Nigerian Society of Physical Sciences: Volume 6, Issue 2, May 2024
- Mariya Helen, Prabhakar V, Computational investigation of free convection flow inside inclined square cavities , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 2, May 2022
- F. O. Akinpelu, R. A. Oderinu, A. D. Ohaegbue, Analysis of Hydromagnetic Double Exothermic Chemical Reactive Flow with Convective Cooling through a Porous Medium under Bimolecular Kinetics , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 1, February 2022
- Uthumporn Panitanarak, Aliyu Ismail Ishaq, Alfred Adewole Abiodun, Hanita Daud, Ahmad Abubakar Suleiman, A new Maxwell-Log logistic distribution and its applications for mortality rate data , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 2, May 2025
- Yakubu Aliyu, Umar Usman, On Bivariate Nadarajah-Haghighi Distribution derived from Farlie-Gumbel-Morgenstern copula in the Presence of Covariates , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 2, May 2023
You may also start an advanced similarity search for this article.






