Jensen-based New Cryptographic Scheme

S. A. Osikoya; E. O. Adeyefa

doi:10.46481/jnsps.2022.325

Authors

S. A. Osikoya
samuelabidemi2@gmail.com
Department of Mathematics, Faculty of Science, Federal University Oye-Ekiti, Ekiti State, Nigeria
E. O. Adeyefa Department of Mathematics, Faculty of Science, Federal University Oye-Ekiti, Ekiti State, Nigeria

Keywords:

Jensen Polynomials, Laplace Transform, Cryptographic algorithm, Information security, Cryptographic Scheme

Abstract

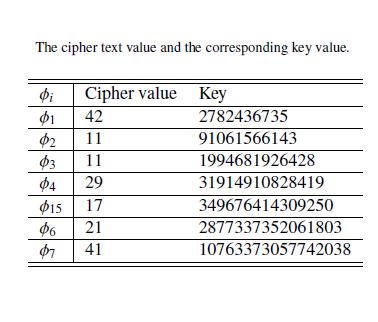
The surgent availability of data and the demand for more data to implement several technological products which heavily depends on data have made the issue of cyber attacks, a global threat, of great concern. To ensure the protection of information, the heart of every nation, the development of formidable techniques which contribute to the advancement of present schemes is crucial to combat the challenge. In this research work, a mathematical framework, from the idea of cryptography, is developed using Jensen polynomial. Jensen polynomial is used for the encryption algorithm, and the Laplace transform is used as a transformation tool to convert the plain text message to cipher text message. The decryption is a reversal which involves the use of structured mathematical techniques and the key for the message.

Dimensions

REFERENCES

A. P. Hiwarekar, “Application of Laplace transform for cryptographic scheme”, Proceedings of world congress on Engineering, 1 (2013) 95.

C. Jayanthi & V. Srinivas, “Mathematical Modeling for Cryptography using Laplace Transform”,International Journal of Mathematical Trends and Technology, 2 (2019) 10. DOI: https://doi.org/10.14445/22315373/IJMTT-V65I2P503

E. O. Adeyefa, L. S. Akinola, & O. D. Agbolade, “A New Cryptographic Scheme Using Chebyshev Polynomials”, 2020 International Conference in Mathematics, Computer Engineering (ICMCECS), (2020) 3. DOI: https://doi.org/10.1109/ICMCECS47690.2020.240868

A. Mittal & R.Gupta, “Kamal transformation based cyrptography technique in network security involving ASCII value”, International Journal of Innovative Technology and Exploring Engineering, 8 (2019) 3448. DOI: https://doi.org/10.35940/ijitee.L2592.1081219

D. Swati, A. Archana and J. Swati, “Laplace transformation based cryptographic technique in network security”, International Journal of Computer Applications, 7 (2016) 10.

M. Saha, “Application of Laplace-Mellin transform for cryptography”, Rai Journal of Technology, Research and Innovation, 1 (2017) 12.

B. D. Gupta, “Mathematical Physics”, Ist ed., reprint, Ansari Road, New Delhi: India, (1980).

M. Griffin, K. Ono, L. Rolen & D. Zagier, “Jensen Polynomials for the Riemann Zeta Function and Other Sequences”, (2019). DOI: https://doi.org/10.1073/pnas.1902572116

G. Nagalakshmi, S. A. Chandra, & S. N. Ravi, “An Implementation of ElGamal Scheme for Laplace Transform Cryptosystem”, Indian Journal of Computer Science and Engineering (IJCSE, 1 (2020) 48. DOI: https://doi.org/10.21817/indjcse/2020/v11i1/201101032

J. P. Aumasson, “Serious Cryptography: A Practical Introduction to Modern Encryption”, (2018).