A New Special 15-Step Block Method for Solving General Fourth Order Ordinary Differential Equations

Authors

  • Victor Oboni Atabo Department of Mathematics, Ahmadu Ribadu College, Yola, Nigeria
  • Solomon Ortwer Adee Department of Mathematics, Modibbo Adama University, Yola, Nigeria

Abstract

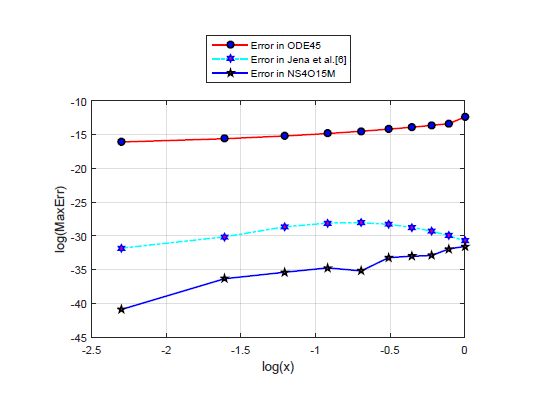
 A new higher-implicit block method for the direct numerical solution of fourth order ordinary differential equation is derived in this research paper. The formulation of the new formula which is 15-step, is achieved through interpolation and collocation techniques. The basic numerical properties of the method such as zero-stability, consistency and A-stability have been examined. Investigation showed that the new method is zero stable, consistent and A-stable, hence convergent. Test examples from recent literature have been used to confirm the accuracy of the new method.

Dimensions

R. Conti, D. Graffi & G. Sansone, Theory of Nonlinear Ordinary Differential Equations, Proc. Internat. Sympos. Non-linear vibrations (1961).

D. Raymond, Y. Skwame & L. Adiku, “Four-step one hybrid block methods for solution of fourth derivative ordinary differential equations”, Journal of Advances in Mathematics and Computer Science 36 (2021) 3. https://doi.org/10.9734/JAMCS/2021/v36i330343

O. E. Abolarin, J. O. Kuboye, E. O. Adeyefa & B. G. Ogunware, “New efficient numerical model for solving second, third and fourth order ordinary differential equations directly”, Gazi University Journal of Science 33 (2020). https://doi.org/10.35378/gujs.627677.

R.Allogmany, F. Ismail, Z. A. Majid &Z.B.Ibrahim, “Implicit two-point block method for solving fourth-order initial value problem directly with application”, Hindawi Mathematical Problems in Engineering (2020). https://doi.org/10.1155/2020/6351279

J. O. Kuboye, “Block methods for higher order ordinary differential equations using interpolation and collocation approach”, [Doctor of Philosophy, University Utara, Malaysia] (2015).

S. R. Jena, M. Mohanty & S. K. Mishra, “Ninth step block method for numerical solution of a fourth order ordinary differential equation”, Advances in Modelling and Analysis 2 (2018) 47. https://doi.org/iieta.org/journals/AMA/AMA.

L. O. Adoghe & E. O. Omole, “A fifth-fourth continuous block Implicit hybrid method for the solution of third order initial value problems in ordinary differential equations”, Journal of Applied and Computational Mathematics 8 (2019) 50. https://doi.org/10.9734/JAMCS/2019/44846.

Z. Omar & J. O. Kuboye, “New seven-step numerical method direct solution of fourth order ordinary differential equations”, ITB Journal Publisher, 48 (2016) 2. https://doi.org/10.5614/j.math.fund.sc.2016.48.2.1.

M.K.Duromola, “An Accurate five off-step points implicit block method for direct solution of fourth order differential equations”, Open Access Library Journal 6 (2016) 1. https://doi.org/10.4236/oalib.1102667.

A. O. Adesanya, A. A. Momoh, M. Adamu & A. Tahir, “Five steps block method for the solution of fourth order ordinary differential equations”, International Journal of Engineering Research and Applications 5 (2012) 991. www.ijera.com

D. O. Awoyemi, S. J. Kayode & L. O. Adoghe, “A six step continuous multistep method for the solution of general fourth order initial value problems of ordinary differential equations”, Journal of Natural Sciences Research 5 (2015) 131.

D. O. Awoyemi, “Algorithmic collocation approach for direct solution fourth order ordinary differential equations”, International Journal of Computer and Mathematics 82 (2005) 321. https://doi.org/10.1080/00207160412331296634.

L. A. Ukpebor, E. O. Omole & L. O. Adoghe, “An order four numerical scheme for fourth-order initial value problems using Lucas polynomial with application in ship dynamics”, International Journal of Mathematical Research 1 (2020) 28.https://doi.org/10.18488/journal.24.2020.91.28.41.

E. O. Omole & L. A. Ukpebor, “A step by step guide on the derivation and analysis of a new numerical method for solving fourth order ordinary differential equations”, Mathematics Letters 2 (2020) 13.https://doi.org/10.11648/j.ml.20200602.12.

J. O. Kuboye, O. R. Elusakin & O. F. Quadri, “Numerical algorithms for direct solution of fourth order ordinary differential equations”, Nigerian Society of Physical Sciences 4 (2020) 218. https://doi.org/10.46481/jnsps.2020.100

L. O. Adoghe & E. O. Omole, “A two-step hybrid block method for the numerical integration of higher order initial value problems of ordinary differential equations”, World scientific news 118 (2019) 236.www.worldscientificnews.com

A. Familua & E. Omole, “Five points mono hybrid point linear multistep method for solving nth order ordinary differential equations using power series function”, Asian Research Journal of Mathematics 3 (2017) 1.https://doi.org/10.9734/ARJOM/2017/31190

P. Henrici, Discrete variable methods in ordinary differential equations, John Wiley and Sons. (1963)

S. Kayode, M. Duromola, & B. Bolaji, “Direct solution of initial value problems of fourth order ordinary differential equations using modified implicit hybrid block method”, Journal of Scientific Research and Reports 3 (2014) 2790.https://doi.org/10.9734/JSRR/2014/11953

J. D. Lambert, Numerical methods for ordinary differential systems, New York: John Wiley. (1991)

J. D. Lambert, Computational methods in ODEs, New York: John Wiley and Sons. (1973)

R. I. Okhuonghae & M. N. O. Ikhile, “A family of highly stable second derivative block methods for stiff IVPs in ODEs”, Numerical Analysis and Applications. Pleiads Publishing Ltd. 7 (2012) 57. https://doi.org/10.1134/S1995423914010066.

Published

2021-11-29

How to Cite

A New Special 15-Step Block Method for Solving General Fourth Order Ordinary Differential Equations. (2021). Journal of the Nigerian Society of Physical Sciences, 3(4), 308-333. https://doi.org/10.46481/jnsps.2021.337

Issue

Volume 3, Issue 4, November 2021

Section

Original Research
Copyright & Licensing

Copyright (c) 2021 Journal of the Nigerian Society of Physical Sciences

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

A New Special 15-Step Block Method for Solving General Fourth Order Ordinary Differential Equations. (2021). Journal of the Nigerian Society of Physical Sciences, 3(4), 308-333. https://doi.org/10.46481/jnsps.2021.337