Higher order Motional Resonances Spectra of electrons with Non-linear Axial Oscillations in Quadrupole Penning trap
Keywords:
Quadrupole Penning trap, Motional resonance spectrum, quadrupole potential, Duffing oscillator, non-linear oscillatorAbstract
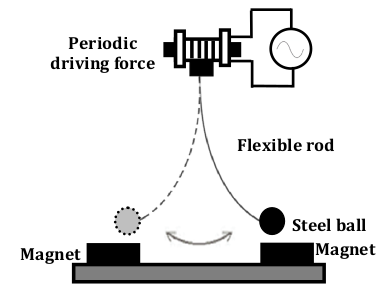
Experimentally the motional resonances spectra of an electron cloud confined in a quadrupole Penning trap, weakly excited with RF field, which is swept from 1 MHz to 1 GHz was examined. The higher order motional resonances of the electron cloud with non-linear axial oscillations show that they result from couplings in the motional degrees of freedom, which characterize the perturbations in the trap, and cause loss of electrons from the trap. The likely presence of perturbative terms of quadrupole potential is identified by studying the motional resonances spectra and hence the multipole terms are calculated. A periodically forced barrel spring with a steel ball at the free end can be regarded as a model of non-linear oscillator and a periodically forced steel ball hung through a flexible rod, which is deflected alternately toward the two magnets can be regarded as a mechanical model of Duffing oscillator are developed, in analogy to observed higher order motional resonances of the electron cloud excited with different RF field powers.
Published
How to Cite
Issue
Section
Copyright (c) 2022 Journal of the Nigerian Society of Physical Sciences

This work is licensed under a Creative Commons Attribution 4.0 International License.







