Application of the Exponentiated Log-Logistic Weibull Distribution to Censored Data

Authors

  • Adeniyi F. Fagbamigbe Department of Epidemiology and Medical Statistics, College of Medicine, Faculty of Public Health, University of Ibadan, Nigeria
  • Gomolemo K. Basele Department of Mathematics and Statistical Sciences, Botswana International University of Science and Technology, Palapye, BW
  • Boikanyo Makubate Department of Mathematics and Statistical Sciences, Botswana International University of Science and Technology, Palapye, BW
  • Broderick O. Oluyede Department of Mathematical Sciences, Georgia Southern University, Statesboro, GA, 30460, USA

Keywords:

Generalized Distribution, Exponentiated log-logistic Distribution, Weibull Distribution, Survival Analysis.

Abstract

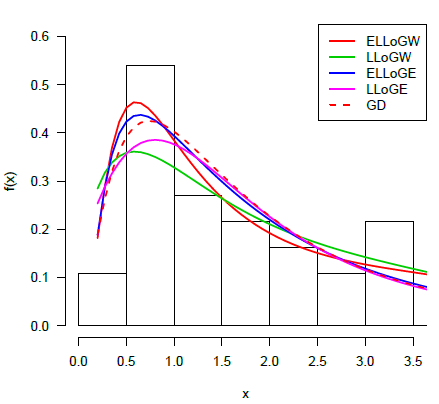
In a recent paper, a new model called the Exponentiated Log-Logistic Weibull (ELLoGW) distribution with applications to reliability, survival analysis and income data was proposed. In this study, we applied the recently developed ELLoGW model to a wide range of censored data. We found that the ELLoGW distribution is a very competitive model for describing censored observations in life-time reliability problems such as survival analysis. This work shows that in certain cases, the ELLoGW distribution performs better than other parametric model such as the Log-Logistic Weibull, Exponentiated Log-Logistic Exponential, Log-Logistic Exponential distributions and the non-nested Gamma-Dagum (GD).

Dimensions

B. O. Oluyede, G. Basele, S. Huang & B. Makubate, “A New Class of Generalized Log-Logistic Weibull Distribution: Theory, Properties and Applications”, Journal of Probability and Statistical Sciences, 14 (2016) 171.

D. Cox, “Regression Models and Life Tables (with Discussion)”, Journal of the Royal Statistical Society, Series B 34 (1972) 187.

P. Mdlongwa, B. O. Oluyede, A. K. A. Amey, A. F. Fagbamigbe & B. Makubate, “Kumaraswamy Log-logistic Weibull Distribution: Model, Theory and Application to Lifetime and Survival Data”, Heliyon 5 (2019) 1.

E. T. Lee & J. Wang, Statistical Methods for Survival Data Analysis, Wiley, New York, 1st Ed. (2003) 1.

B. O. Oluyede, B. Makubate, A. F. Fagbamigbe & P. Mdlongwa, “A New Burr XII-Weibull-Logarithmic Distribution for Survival and Lifetime Data Analysis: Model, Theory & Applications. Stats 1 (2018) 77.

M. Pararai, G. Warahena-Liyanage & B. O. Oluyede, “A New Class of Generalized Power Lindley Distribution with Applications to Lifetime Data”, Theoretical Mathematics & Applications 5 (2015) 53.

J. P. Klein & M. L. Moeschberger Survival Analysis Techniques for Censored and Truncated Data, Springer-Verlag, New York, 2003.

W. H. Alven Reliability Engineering by ARINC, Prentice-Hall, New Jersey, 1964.

R. S. Chikara & J. L. Folks, “The Inverse Gaussian Distribution as a Lifetime Model”, Technometrics 19 (1977) 461.

T. Dimitrakopoulou, K. Adamidis & S. Loukas, “A Lifetime Distribution with an Upside-Down Bathtub-Shaped Hazard Function”, IEEE Transactions on Reliability 56 (2007) 308.

B. O. Oluyede & S. Huang, “Estimation in the Exponentiated Kumaraswamy Dagum Distribution with Censored Samples”, Electronic Journal of Applied Statistical Analysis 8 (2016) 122.

T. S. Ferguson, A Course in Large Sample Theory, Chapman & Hall (1996).

B. O. Oluyede, S. Huang & M. Pararai, “A New Class of Generalized Dagum Distribution with Applications to Income and Lifetime Data”, Journal of Statistical and Econometric Methods 3 (2014) 125.

Published

2019-03-31

How to Cite

Application of the Exponentiated Log-Logistic Weibull Distribution to Censored Data. (2019). Journal of the Nigerian Society of Physical Sciences, 1(1), 12-19. https://doi.org/10.46481/jnsps.2019.4

Issue

Volume 1, Issue 1, February 2019

Section

Original Research
Copyright & Licensing

Copyright (c) 2019 Journal of the Nigerian Society of Physical Sciences

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Application of the Exponentiated Log-Logistic Weibull Distribution to Censored Data. (2019). Journal of the Nigerian Society of Physical Sciences, 1(1), 12-19. https://doi.org/10.46481/jnsps.2019.4