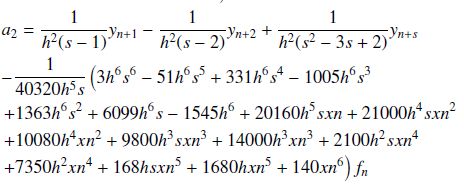Solving third order ordinary differential equations directly using hybrid numerical models
Keywords:
Interpolation, collocation, block method, multistep method and third order initial value problemAbstract
In this work, numerical methods for solving third order initial value problems of ordinary differential equations are developed. Multi-step collocation is used in deriving the methods, where power series approximate solution is employed as a basis function. Gaussian elimination approach is considered in finding the unknown variables $a_j, j=0(1)8$ in interpolation and collocation equations, which are substituted into the power series to give the continuous implicit schemes. The discrete schemes and its derivatives are derived by evaluating the grid and non-grid points. These schemes are arranged in a matrix form to produce block methods. The order of the developed methods are found to be six. The numerical results proved the efficiency of the methods over the existing methods.