Comparison of the Solution of the Van der Pol Equation Using the Modified Adomian Decomposition Method and Truncated Taylor Series Method

Authors

  • Joel Ndam Department of Mathematics, University of Jos, Nigeria
  • O. Adedire Federal College of Forestry, Jos, Nigeria

Keywords:

van der Pol oscillator, modified Adomian decomposition method, Taylor series method

Abstract

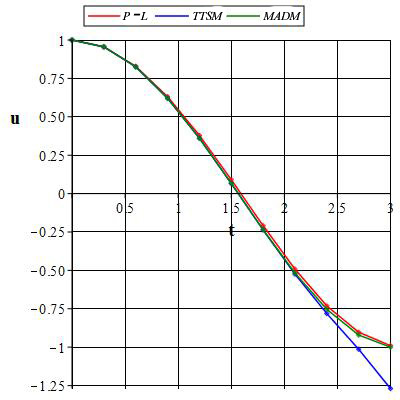
In this paper, we compare the solution of the van der Pol equation obtained by using the truncated Taylor series method and the modified Adomian decomposition method with the solution obtained by the Poincare-Lindstedt (P-L) method. The approximating 4-component modified Adomian decomposition method behaves more like an approximate P-L analytic method than the tenth-order Taylor series. Also, with the addition of just one term, the approximating 5-component modified Adomian decomposition method produces a more convergent solution to that of P-L analytic method than the twenty second-order Taylor series approximation as the independent variable t representing time progressively increases. A general comparison of the two solutions revealed that the absolute errors generated by the approximating polynomial from the Taylor series are greater than the ones generated from the modified Adomian decomposition method. It was further revealed that very few components of the modified Adomian decomposition could yield a series of about 3 times the order of the one obtained by using the Taylor series method. Hence, we recommend the inclusion of the modified Adomian Decomposition Method in modern mathematical tools.

Dimensions

E. A. Az-Zobi, K. Al-Khaled & A. Darweesh, “Numeric-Analytic solutions for nonlinear oscillators via the modified multi-stage decomposition method.”, MDPI Journal of Mathematics 7 (2019) 1. doi:10.3390/math7060550

J. Biazar and Y. Shafiof, “A simple algorithm for calculating Adomian polynomials. Int. J. Contemp. Math. Sciences, 975 - 982.

Y. Daoud & A. A. Khidir, “Modified Adomian decomposition method for solving the problem of boundary layer convective heat transfer",Journal of Propulsion and Power Research 7 (2018) 231. doi: 10.1016/j.jppr.2018.05.005

I. L. El-Kalla, “Error analysis of Adomian series solution to a class of nonlinear differential equations”, Applied Mathematics E-notes 7 (2007) 214.

H. Gundogdu & O. F. Gozukizil, “Solving nonlinear partial differential equations by using Adomian decomposition method, modified decomposition method and Laplace decomposition method”, MANAS Journal of Engineering 5 (2017) 1.

J. H. He, “Modified Lindstedt-Poincare methods for some strongly non-linear oscillations. Part 1: expansion of a constant”, International Journal of nonliear mechanics 37 (2002) 309. doi: 10.1016/S0020-7462(00)00116-5

K. G. Howison, Practical Applied Mathematics: Modelling, Analysis, Approximation”, (2005) Cambridge University Press, United Kingdom.

B. Jang, “Two-point boundary value problems by the extended Adomian decomposition method”, J. Comput. Appl. Math 219 (2008) 253. doi:10.1016/j.cam.2007.07.036

K. K. Kataria & P. Vellisamy, “Simple parameterization methods for generating Adomian polynomials”, Applicable analysis and discrete Mathematics 10 (2016) 168. doi:10.2298/AADM160123001K

J. D. Logan, Applied Mathematics., (2006) John Wiley.

P. J. Melvin, “On the construction of Poincare-Lindstedt solutions: The nonlinear oscillator equation”, SIAM Journal of Applied Mathematics 33 (1977) 161. doi:10.1137/0133011

D E. Panayotounakos, N. D. Panayotounakou & P. S. Vakakis, “On the lack of analytic solutions of the van der Pol Oscillator, ZAMM- Journal of Applied Mathematics and Mechanics 83 (2003) 611. doi:10.1002/zamm.200310040

Y. W. Putranto & S. Mungkasi, “Adomian decomposition method for solving population dynamics model of two species”, Journal of Physics: Conference Series 795 (2017) 1. doi: 10.1088/1742-6596/795/1/012045

U. Saeed, “Haar Adomian method for the solution of Fractional Nonlinear Lane-Emden type equations arising in astrophysics”, Taiwanese Journal of Mathematics 21 (2017) 1175. doi:10.11650/tjm/7969

A. S. Soomro, G. A. Tularam & M. M. Shaikh, “A comparison of Numerical Methods for Solving the Unforced Van Der Pol’s Equation”, Mathematical Theory and Modelling 3 (2017).

D. Viswannath, “The construction of Lindstedt-Poincare technique as an algorithm for computing periodic orbits, SIAM Journal of Applied Mathematics 43 (2001) 478. doi: 10.1137/s0036144500375292

A. M.Wazwaz, “A comparison between Adomian decomposition method and Taylor series method in the series solutions”, Appl. Math. Comput 97 (1998) 37. doi: 10.1016/S0096-3003(97)10127-8

A. M. Wazwaz “A new algoritm for calculating Adomian polynomials for nonlinear operators”, Appl. Math. Comput 111 (2000) 53. doi: 10.1016/S0096-3003(99)00063-6

A. M. Wazwaz & A. Gorguis, “An analytic study of Fisher’s equation by using Adomian decomposition method”, Appl. Math. Comput 154 (2004) 609. doi: 10.1016/S0096-3003(03)00738-0

Published

2020-05-13

How to Cite

Comparison of the Solution of the Van der Pol Equation Using the Modified Adomian Decomposition Method and Truncated Taylor Series Method. (2020). Journal of the Nigerian Society of Physical Sciences, 2(2), 106-114. https://doi.org/10.46481/jnsps.2020.44

Issue

Volume 2, Issue 2, May 2020

Section

Original Research
Copyright & Licensing

How to Cite

Comparison of the Solution of the Van der Pol Equation Using the Modified Adomian Decomposition Method and Truncated Taylor Series Method. (2020). Journal of the Nigerian Society of Physical Sciences, 2(2), 106-114. https://doi.org/10.46481/jnsps.2020.44