Exponentially Fitted Chebyshev Based Algorithm as Second Order Initial Value Solver

Authors

  • Emmanuel Adeyefa Mathematics Department, Faculty of Science, Federal University Oye-Ekiti, Ekiti State, Nigeria
  • O. S. Esan Mathematics Department, Faculty of Science, Federal University Oye-Ekiti, Ekiti State, Nigeria

Keywords:

Chebyshev polynomial, Convergence, IVPs, Numerical Integrator, ODEs

Abstract

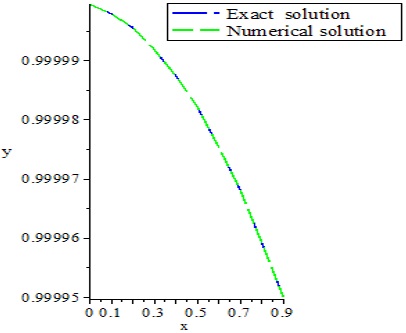
In this research work, we focus on development of a numerical algorithm which is well suited as integrator of initial value problems of order two. Exponential function is fitted into the Chebyshev polynomials for the formulation of this new numerical integrator. The efficiency, ingenuity and computational reliability of any numerical integrator are determined by investigating the zero stability, consistency and convergence of the integrator. Findings reveal that this algorithm is convergent. On comparison, the solutions obtained through the algorithm compare favourably well with the analytical solutions.

Dimensions

J. C. Butcher “A modified Multistep Method for the Numerical Integration of Ordinary Di erential Equations”, Journal of the ACM, 12 (1965) 124.

J. D. Lambert “Computational methods in Ordinary di erential system”, John Wiley, New York (1973).

J. D. Lambert “Numerical Methods for Ordinary Differential Systems”, John Wiley, New York (1991).

P. Henrici “Discrete Variable Methods in ODE”, New York, John Wiley and Sons (1962).

E. O. Adeyefa “Orthogonal-based hybrid block method for solving general second order initial value problems”, Italian journal of pure and applied mathematics 37 (2017) 659.

S. N. Jator & E. O. Adeyefa “Direct Integration of Fourth Order Initial and Boundary Value Problems using Nystrom Type Methods”, IAENG

International Journal of Applied Mathematics 49 (2019) 638.

S. N Jator & J. Li “A self-starting linear multistep method for a direct solution of the general second order initial value problem”, International Journal of Computational Mathematics 86 (2009) 827.

E. A. Ibijola “New Schemes for Numerical Integration of Special Initial Value Problems in Ordinary Differential Equations”, Ph.D. Thesis, University of Benin, Nigeria (1997).

E. A. Ibijola & P. Kama “On the convergence, consistency and stability of A new One-Step Method for Numerical integration of ODE”, International Journal of Computational Mathematics 73 (1999) 261.

O. O. Enoch & A. A. Olatunji: “A New Self-Adjusting Numerical Integrator for the Numerical Solutions of Ordinary Differential Equations”, Global Journal GJSFR 12 (2012) 1022.

S. O. Ayinde & E. A. Ibijola “A new numerical method for solving first order differential equations”, American journal of applied mathematics and statistics 3 (2015) 156.

O. O. Enoch & E. A. Ibijola “A Self-Adjusting Numerical Integrator with an inbuilt Switch for Discontinuous Initial Value Problems”, Australian Journal of Basic and Applied Sciences 5 (2011) 1560.

S. O. Fatunla “Numerical methods for IVPs, in ODEs”, Academic press. USA (1988).

S. O. Fatunla “A new Algorithm for numerical solution of ODEs. Computer and Mathematics with Applications”, 2 (1976) 247.

Published

2020-03-05

How to Cite

Exponentially Fitted Chebyshev Based Algorithm as Second Order Initial Value Solver. (2020). Journal of the Nigerian Society of Physical Sciences, 2(1), 51-54. https://doi.org/10.46481/jnsps.2020.45

Issue

Volume 2, Issue 1, February 2020

Section

Original Research
Copyright & Licensing

How to Cite

Exponentially Fitted Chebyshev Based Algorithm as Second Order Initial Value Solver. (2020). Journal of the Nigerian Society of Physical Sciences, 2(1), 51-54. https://doi.org/10.46481/jnsps.2020.45