A Higher-order Block Method for Numerical Approximation of Third-order Boundary Value Problems in ODEs

Adefunke Bosede Familua; Ezekiel Olaoluwa Omole; Luke Azeta Ukpebor

doi:10.46481/jnsps.2022.706

Authors

Adefunke Bosede Familua
Department of Mathematics and Statistics, First Technical University, Ibadan, Oyo State, Nigeria
Ezekiel Olaoluwa Omole
[email protected]

Department of Mathematics and Statistics, Joseph Ayo Babalola University, Ikeji Arakeji, Osun State, Nigeria; Department of Mathematics, Federal University Oye-Ekiti, Ekiti State, Nigeria
Luke Azeta Ukpebor
Department of Mathematics, Ambrose Alli University Edo State, Nigeria

Keywords:

Convergence analysis, Linear & nonlinear problems, Ordinary differential equations, Power series basic function, Third-order boundary value problems

Abstract

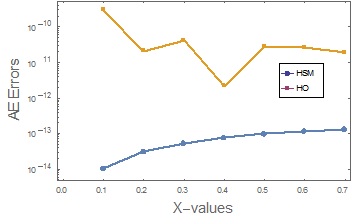
In recent times, numerical approximation of 3rd-order boundary value problems (BVPs) has attracted great attention due to its wide applications in solving problems arising from sciences and engineering. Hence, A higher-order block method is constructed for the direct solution of 3rd-order linear and non-linear BVPs. The approach of interpolation and collocation is adopted in the derivation. Power series approximate solution is interpolated at the points required to suitably handle both linear and non-linear third-order BVPs while the collocation was done at all the multiderivative points. The three sets of discrete schemes together with their first, and second derivatives formed the required higher-order block method (HBM) which is applied to standard third-order BVPs. The HBM is self-starting since it doesn’t need any separate predictor or starting values. The investigation of the convergence analysis of the HBM is completely examined and discussed. The improving tactics are fully considered and discussed which resulted in better performance of the HBM. Three numerical examples were presented to show the performance and the strength of the HBM over other numerical methods. The comparison of the HBM errors and other existing work in the literature was also shown in curves.

Dimensions

REFERENCES

S. N. Jator, “Multiple finite di erence methods for solving third order ordinary differential equations”, International Journal of Pure and Applied Mathematics 43 (2007) 253.

S. N. Jator, “Novel finite difference schemes for third order boundary value problems”, Intern. J. Pure and Appl. Math. 53 (2009) 37.

D. O. Awoyemi, “A P-stable linear multistep method for solving general third order ordinary differential equations”, Intern. J. Comput. Math. 80 (2003) 987.

E. O. Omole & B. G. Ogunware, “3- Point single hybrid block method (3PSHBM) for direct solution of general second order initial value problem of ordinary differential equations”, Journal of Scientific Research and Reports 20 (2018) 1.

V. O. Ataboa & S. O. Adee, “A new special 15-step block method for solving general fourth order ordinary differential equations”, J. Nig. Soc. Phys. Sci. 3 (2021) 308, https://doi.org/10.46481/jnsps.2021.337.

A. O. Adeniran, S. A. Odejide, B. S. & Ogundare, “One step hybrid numerical scheme for the direct solution of general second order ordinary differential equations”, International Journal of Applied Mathematics 28 (2015) 197, http://dx.doi.org/10.12732/ijam.v28i3.2

K. E. Atkinson, An introduction to numerical analysis, 2nd edition John Wiley and Sons, New York (1989).

Familua A. B., “Direct approach for solving second order delay differential equations through a five-step with several o -grid points”, International Journal of Applied Mathematics and Theoretical Physics 8 (2022) 1, https://doi.org/10.11648/j.ijamtp.20220801.11

A. Shokri & M. Tahmourasi, “A new two-step Obrechkoff method with vanished phase-lag and some of its derivatives for the numerical solution of radial Schrodinger equation and related IVPs with oscillating solutions”, Iranian Journal of Mathematical Chemistry 8 (2017) 137.

V. J. Shaalinia & S. E. Fadugba, “A new multi-step method for solving delay differential equations using Lagrange interpolation”, J. Nig. Soc.Phys. Sci. 3 (2021) 159, https://doi.org/10.46481/jnsps.2021.247.

A. Shokri, “An explicit trigonometrically fitted ten-step method with phase-lag of order infinity for the numerical solution of the radial Schrodinger equation”, Applied and Computational Mathematics 14 (2015) 63.

Y. Skwame, J. Sabo & M. Mathew, “The treatment of second order ordinary differential equations using equidistant one-step block hybrid”, Asian Journal of Probability & Statistics 5 (2019) 1.

A. Shokri, J. Vigo-Aguiar, K. M. Khalsaraei & R. Garcia-Rubio, “A new implicit six-step P-stable method for the numerical solution of Schr¨odinger equation”, International Journal of Computer Mathematics 97 (2020) 802.

M. Kida, S. Adamu, O. O. Aduroja & T. P. Pantuvo, “Numerical solution of stiff and oscillatory problems using third derivative trigonometrically fitted block method”, J. Nig. Soc. Phys. Sci. 4 (2022) 34, https://doi.org/10.46481/jnsps.2022.271.

J. O. Kuboye, O. R. Elusakin & O. F. Quadri, “Numerical algorithms for direct solution of fourth order ordinary differential equations”, J. Nig. Soc. Phys. Sci. 2, (2020) 218, https://doi.org/10.46481/jnsps.2020.100.

B. G. Ogunware, E. O. Omole & O. O. Olanegan, “Hybrid and non- hybrid implicit schemes for solving third order ODEs using block method as predictors”, Journal of Mathematical Theory & Modelling (iiste) 5 (2015) 10.

B. G. Ogunware & E. O. Omole, “A class of irrational linear block method for the direct numerical solution of third order ordinary differential equations”, Turkish Journal of Analysis and Number Theory 8 (2020) 21, https://doi.org/10.12691/tjant-8-2-1.

J. D. Lambert, Computational methods in ordinary differential equations, John Wiley & Sons Inc. (1973).

A. A. Aigbiremhon & E. O. Omole, “A Four-step Collocation Procedure by means of perturbation term with application to third-order ordinary differential equations”, International Journal of Computer Applications 174 (2020) 25.

B. I. Akinnukawe & K. O. Muka, “L-Stable block hybrid numerical algorithm for first-order ordinary differential equations”, J. Nig. Soc. Phys. Sci. 2 (2020) 160.

E. O. Omole, O. A. Jeremiah & L. O. Adoghe, “A class of continuous implicit seventh-eight method for solving y0 = f (x; y) using power series as basic function”, International Journal of Chemistry, Mathematics and Physics (IJCMP) 4 (2020) 39, https://dx.doi.org/10.22161/ijcmp.4.3.2.

A. Shokri, J. Vigo-Aguiar, M. M. Khalsaraei & R. Garcia-Rubio, “A new four-step P-stable Obrechkoff method with vanished phase-lag and some of its derivatives for the numerical solution of radial Schr¨odinger equation”, Journal of Computational and Applied Mathematics 354 (2019) 569.

A. Shokri & A. A. Shokri, “Implicit one-step L-stable generalized hybrid methods for the numerical solution of first order initial value problems”, Iranian Journal of Mathematical Chemistry 4 (2013) 201.

B. G. Ogunware, L. O. Adoghe, D. O. Awoyemi, O. O. Olanegan & E. O. Omole, “Numerical treatment of general third order ordinary differential equations using Taylor series as predictor”, Physical Science International Journal 17 (2018) 1, https://doi.org/10.9734/PSIJ/2018/22219.

O. A. Akinfenwa, S. A. Okunuga, B. I. Akinnukawe, U. P. Rufai & R. I. Abdulganiy, “Multi-derivative hybrid implicit Runge-Kutta method for solving stiff system of a first order differential equation”, Far East Journal of Mathematical Sciences (FJMS) 106 (2018) 543.

R. Abdelrahim, “Numerical solution of third order boundary value problems using one-step hybrid block method”, Ain Shams Engineering Journal 10 (2019) 179.

D. Faires & R. L. Burden, Numerical methods, 2nd ed. International Thomson Publishing Inc. (1998).

L. O Adoghe & E. O. Omole, “A fifth-fourth continuous block implicit hybrid method for the solution of third order initial value problems in ordinary differential equations”, Journal of Applied and Computational Mathematics 8 (2019) 50, https://doi.org/10.11648/j.acm.20190803.11.

L. O. Adoghe, B. G. Ogunware & E. O. Omole, “A family of symmetric implicit higher order methods for the solution of third order initial value problems in ordinary differential equations”, Journal of Theoretical Mathematics & Applications 6 (2016) 67.

J. Ahmed, “Numerical solutions of third-order boundary value problems associated with draining and coating flows”, Kyungpook Mathematical Journal 57 (2017) 651, https://doi.org/10.5666/KMJ.2017.57.4.651.

F. A. A. El-Salam, A. A. El-Sabbagh & Z. A. Zaki, “The numerical solution of linear third-order boundary value problems using nonpolynomial spline technique”, J. American. Sci. 6 (2010) 303.

A. Khan & T. Aziz, “The numerical solution of third-order boundary value problems using quintic splines”, Appl. Math. Comput. 137 (2003) 253.

L. Zhiyuan, Y. Wang & F. Tan, “The solution of a class of third-order boundary value problems by the reproducing kernel method”, Abs. Appl. Anal. 1 (2012) 1.

A. S. Abdullah, Z. A. Majid & N. Senu, “Solving third order boundary value problem with fifth order block method”, Math. Meth. Eng. Econ. 1 (2014) 87.

T. S. El-Danaf, “Quartic nonpolynomial spline solutions for third order two-point boundary value problem”, World Acad. Sci. Eng. Technology 45 (2008) 453.

P. K. Srivastava&M. Kumar, “Numerical algorithm based on quintic nonpolynomial spline for solving third-order boundary value problems associated with draining and coating flows”, Chin. Ann. Math. 33B (2012) 831.

G. Akram, M. Tehseen, S. S. Siddiqi & H. Rehman, “Solution of a linear third-order multi-point boundary value problem using RKM”, British J. Mat. Comput. Sci. 3 (2013) 180.

M. B. Hossain, M. J. Hossain, S. M. Galib & M. M. H. Sikdar, “The numerical solution of third order boundary value problems using piecewise Bernstein polynomials by the Galerkin weighted residual method”, International Journal of Advanced Research in Computer Science 7 (2016).