A Purusit Differential Game Problem on a Closed Convex Subset of a Hilbert Space
Keywords:
Pursuit, integral constraint, closed convex set.Abstract
We study a pursuit differential game problem with finite number of pursuers and one evader on a nonempty closed convex subset of the Hilbert space l2. Players move according to certain first order ordinary differential equations and control functions of the pursuers and evader are subject to integral constraints. Pursuers win the game if the geometric positions of a pursuer and the evader coincide. We formulated and prove theorems that are concern with conditions that ensure win for the pursuers. Consequently, wining strategies of the pursuers are constructed. Furthermore, illustrative example is given to demonstrate the result.
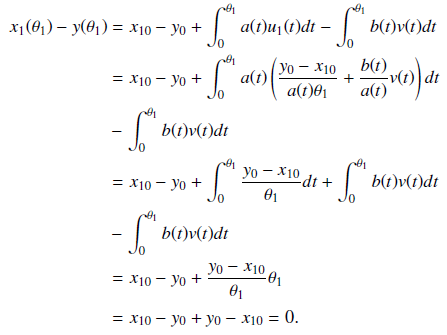
Published
How to Cite
Issue
Section
How to Cite
Similar Articles
- Jamilu Adamu, Aminu Sulaiman Halliru, Bala Ma’aji Abdulhamid, On Some Pursuit Differential Game Problem in a Hilbert Space , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 1, February 2022
- O. T. Wahab, I. F. Usamot, S. M. Alata, K. R. Tijani, On Nonexpansive and Expansive Semigroup of Order-Preserving Total Mappings in Waist Metric Spaces , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 1, February 2023
- Jamilu Adamu, B. M. Abdulhamid, D. T. Gbande, A. S. Halliru, Simple motion pursuit differential game problem of many players with integral and geometric constraints on controls function. , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 1, February 2021
- K. Ahmed, M. Y. Waziri, A. S. Halilu, I. A. R. Moghrab, H. Abdullahi, S. M. Ibrahim, Y. B. Musa, S. Murtala, A. M. Awwal, A. Sambas, A Dai-Kou-Type method with image de-blurring application , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 3, August 2025
- Kazeem adebowale Dawodu, Extension of ADMMAlgorithmin Solving Optimal Control Model Governed by Partial Differential Equation , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 2, May 2021
- Jinta Jose, Rajesh K. Thumbakara, J. D. Thenge Mashale, Bobin George, Sijo P. George, Homomorphic and restricted homomorphic products of soft graphs , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 1, February 2025
- Shehu Shagari Mohammed, On Fuzzy Soft Set-Valued Maps with Application , Journal of the Nigerian Society of Physical Sciences: Volume 2, Issue 1, February 2020
- Jabar Hassan, Haider Majeed, Ghassan Ezzulddin Arif, System of Non-Linear Volterra Integral Equations in a Direct-Sum of Hilbert Spaces , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 4, November 2022
- E. I. Akinola, R. A. Oderinu, S. Alao, O. E. Opaleye, An Integral Transform-Weighted Residual Method for Solving Second Order Linear Boundary Value Differential Equations with Semi-Infinite Domain , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 4, November 2022
- Sunday Emmanuel Fadugba, Solution of Fractional Order Equations in the Domain of the Mellin Transform , Journal of the Nigerian Society of Physical Sciences: Volume 1, Issue 4, November 2019
You may also start an advanced similarity search for this article.






