Collocation Approach for the Computational Solution Of Fredholm-Volterra Fractional Order of Integro-Differential Equations
Keywords:
FREDHOLM-VOLTERRA, Collocation, Integro-differentialAbstract
In this work, a collocation technique is used to determine the computational solution to fractional order Fredholm-Volterra integro-differential equations with boundary conditions using Caputo sense. We obtained the linear integral form of the problem and transformed it into a system of linear algebraic equations using standard collocation points. The matrix inversion approach is adopted to solve the algebraic equation and substituted it into the approximate solution. We established the uniqueness and convergence of the method and some modelled numerical examples are provided to demonstrate the method’s correctness and efficiency. It is observed that the results obtained by our new method are accurate and performed better than the results obtained in the literature. The study will be useful to engineers and scientists. It is advantageous because it addresses the difficulty in tackling fractional order Fredholm-Volterra integro-differential problems using a simple collocation strategy. The approach has the advantage of being more accurate and reducing computer running time.
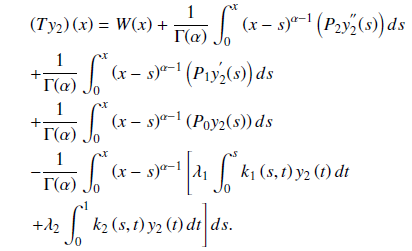
Published
How to Cite
Issue
Section
Copyright (c) 2022 Ganiyu Ajileye, Adewale James, Ayinde Abdullahi, Taiye Oyedepo

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Most read articles by the same author(s)
- G. Ajileye, A. A. James, Collocation Method for the Numerical Solution of Multi-Order Fractional Differential Equations , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 3, August 2023







