Graph Theory: A Lost Component For Development in Nigeria

Authors

Keywords:

Adjacency matrix, Laplacian matrix, dual graph, graph spectrum, graph energy

Abstract

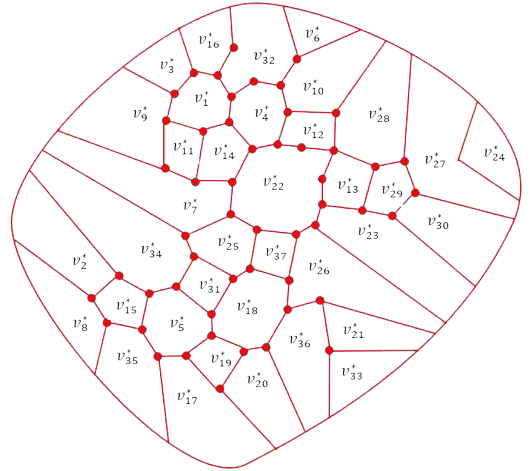
Graph theory is one of the neglected branches of mathematics in Nigeria but with the most applications in other fields of research. This article shows the paucity, importance, and necessity of graph theory in the development of Nigeria. The adjacency matrix and dual graph of the Nigeria map were presented. The graph spectrum and energies (graph energy and Laplacian energy) of the dual graph were computed. Then the chromatic number, maximum degree, minimum spanning tree, graph radius, and diameter, the Eulerian circuit and Hamiltonian paths from the dual graph were obtained and discussed.

Dimensions

G. Chartrand, P. Zhang, A first course in graph theory, Courier Corporation, 2013.

K. H. Rosen, K. Krithivasan, Discrete mathematics and its applications, McGraw-Hill Education, Singapore, 2015.

F. Harary, A seminar on graph theory, Courier Dover Publications, 2015.

H. Sachs, M. Stiebitz, R. J. Wilson, An historical note: Euler's konigsberg letters, Journal of Graph Theory 12 (1988) 133. doi:https://doi.org/10.1002/jgt.3190120114.

S. M. Cioab?a, A first course in graph theory and combinatorics, Vol. 55, Springer, 2009.

J. A. Bondy, U. S. R. Murty, et al., Graph theory with applications, Vol. 290, Macmillan London, 1976.

D. B. West, et al., Introduction to graph theory, Vol. 2, Prentice Hall, 2001.

A. E. Brouwer, W. H. Haemers, Spectra of graphs, Springer Science & Business Media, 2011.

S. Shirinivas, S. Vetrivel, N. Elango, Applications of graph theory in computer science an overview, International journal of engineering science and technology 2 (2010) 4610.

N. Trinajstic, Chemical graph theory, pp. 45–60. doi:https://doi.org/10.1201/9781315139111.

R. Bapat, D. Kalita, S. Pati, On weighted directed graphs,

Linear Algebra and its Applications 436 (2012) 99.

doi:https://doi.org/10.1016/j.laa.2011.06.035.

K. Guo, B. Mohar, Hermitian adjacency matrix of digraphs and mixed graphs, Journal of Graph Theory 85 (2015) 217. doi:https://doi.org/10.1002/jgt.22057.

S. Arumugam, A. Brandst¨adt, T. Nishizeki, K. Thulasiraman, Handbook of graph theory, combinatorial optimization, and algorithms, Chapman and Hall/CRC, 2016.

A. Bickle, Fundamentals of Graph Theory, Vol. 43, American Mathematical Soc., 2020.

O. Babarinsa, H. Kamarulhaili, Mixed energy of a mixed hourglass graph, Communications in Mathematics and Applications 10 (2019) 45. doi:https://doi.org/10.26713/cma.v10i1.1143.

O. Babarinsa, H. Kamarulhaili, Mixed hourglass graph, in: AIP Conference

Proceedings, Vol. 2184, AIP Publishing LLC, 2019, p. 020003. doi:https://doi.org/10.1063/1.5136357.

J. L. Gross, J. Yellen, M. Anderson, Graph theory and its applications,Chapman and Hall/CRC, 2018.

J. M. Harris, J. L. Hirst, M. J. Mossinghoff, Combinatorics and graph theory, Vol. 2, Springer, 2008.

I. Gutman, Chemical Graph Theory: The Mathematical Connection, Vol. 51, Academic Press, 2006, pp. 125–138. doi:https://doi.org/10.1016/S0065-3276(06)51003-2.

V. Nikiforov, The energy of graphs and matrices, Journal of Mathematical Analysis and Applications 326 (2) (2007) 1472–1475. doi:https://doi.org/10.1016/j.jmaa.2006.03.072.

I. Gutman, Hyperenergetic and hypoenergetic graphs, Selected Topics on Applications of Graph Spectra, Math. Inst., Belgrade (2011) 113–135.

O. Babarinsa, H. Kamarulhaili, On determinant of laplacian matrix and signless laplacian matrix of a simple graph, in: International Conference on Theoretical Computer Science and Discrete Mathematics, Vol. 10398, Springer, 2017, pp. 212–217.

D. Kiani, M. Mirzakhah, On the laplacian characteristic polynomials of mixed graphs, Electronic Journal of Linear Algebra 30 (2015) 135. doi:https://doi.org/10.13001/1081-3810.2959.

S. Majstorovic, A. Klobucar, I. Gutman, Selected topics from the theory of graph energy: hypoenergetic graphs, Applications of Graph Spectra, Math. Inst., Belgrade (2009) 65.

Z. Huigang, B. Xiao, Z. Huaxin, Z. Huijie, Z. Jun, C. Jian, L. Hanqing, Hierarchical remote sensing image analysis via graph laplacian energy, IEEE Geoscience and Remote Sensing Letters 10 (2) (2012) 396–400.

E. S. LENI, et al., A technique for classification of high resolution satellite images using object-based segmentation., Journal of Theoretical & Applied Information Technology 68 (2014) 275–286.

I. Gutman, B. Furtula, Graph energies and their applications, Bulletin (Academie serbe des sciences et des arts. Classe des sciences mathematiques et naturelles. Sciences math´ematiques) 44 (2019) 29.

I. Gutman, H. Ramane, Research on graph energies in 2019, MATCH Commun. Math. Comput. Chem 84 (2020) 277.

Published

2022-08-20

How to Cite

Graph Theory: A Lost Component For Development in Nigeria. (2022). Journal of the Nigerian Society of Physical Sciences, 4(3), 844. https://doi.org/10.46481/jnsps.2022.844

Issue

Volume 4, Issue 3, August 2022

Section

Original Research
Copyright & Licensing

Copyright (c) 2022 Olayiwola Babarinsa

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Graph Theory: A Lost Component For Development in Nigeria. (2022). Journal of the Nigerian Society of Physical Sciences, 4(3), 844. https://doi.org/10.46481/jnsps.2022.844