Portfolio Strategy for an Investor with Logarithm Utility and Stochastic Interest Rate under Constant Elasticity of Variance Model

Authors

  • Edikan E. Akpanibah Department of Mathematics and Statistics, Federal University Otuoke, Bayelsa, Nigeria
  • Udeme Ini Department of Mathematics and Computer Science, Niger Delta University, Bayelsa, Nigeria.

Keywords:

Stochastic interest rate, optimal portfolio strategy, asymptotic technique, constant elasticity of variance, logarithm utility

Abstract

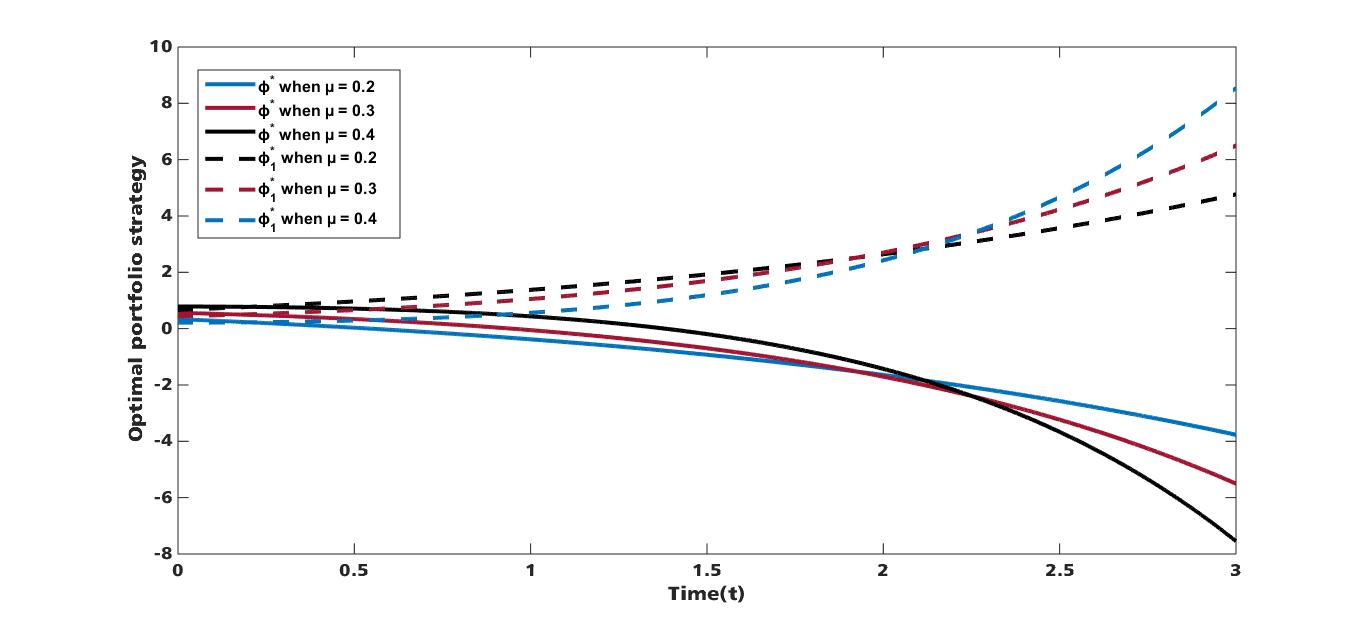
This paper is aim at maximizing the expected utility of an investor’s terminal wealth; to achieve this, we study the optimal portfolio strategy for an investor with logarithm utility function under constant elasticity of variance (CEV) model in the presence of stochastic interest rate. A portfolio comprising of one risk free asset and one risky asset is considered where the risk free interest rate follows the Cox- Ingersoll-Ross (CIR) model and the risky asset is modelled by CEV. Using power transformation, change of Variable and asymptotic expansion technique, an explicit solution of the optimal portfolio strategy and the Value function is obtained. Furthermore, numerical simulations are presented to study the effect of some parameters on the optimal portfolio strategy under stochastic interest rate.

Dimensions

J. C. Cox & S. A. Ross, “The valuation of options for alternative stochastic processes”, Journal of financial economics 3 (1976) 145

D. Li, X. Rong & H. Zhao, “Optimal investment problem with taxes, dividends and transaction costs under the constant elasticity of variance model”, Transaction on Mathematics 12 (2013) 243.

J. Xiao, Z. Hong & C. Qin. “The constant elasticity of variance (CEV) model and the Legendre transform-dual solution for annuity contracts”, Insurance 40 (2007) 302.

J. Gao, “Optimal portfolios for DC pension plan under a CEV model”, Insurance Mathematics and Economics 44 (2009) 479.

M. Gu, Y. Yang, S. Li & J. Zhang, “Constant elasticity of variance model for proportional reinsurance and investment strategies”, Insurance: Mathematics and Economics 46 (2010) 580.

B. O. Osu, E. E. Akpanibah & B. I. Oruh, “Optimal investment strategies for defined contribution (DC) pension fund with multiple contributors via Legendre transform and dual theory”, International journal of pure and applied researches 2 (2017) 97.

D. Li, X. Rong, H. Zhao & B. Yi, “Equilibrium investment strategy for DC pension plan with default risk and return of premiums clauses under CEV model”, Insurance 72 (2017) 6.

E. E. Akpanibah, & O. Ogheneoro, “Optimal Portfolio Selection in a DC Pension with Multiple Contributors and the Impact of Stochastic Additional Voluntary Contribution on the Optimal Investment Strategy”, International journal of mathematical and computational sciences 12 (2018) 14.

J. F. Boulier, S. Huang & G. Taillard, “Optimal management under stochastic interest rates: the case of a protected defined contribution pension fund”, Insurance 28 (2001) 173.

G. Deelstra M. Grasselli & P. F. Koehl, “Optimal investment strategies in the presence of a minimum guarantee”, Insurance 33 (2003) 189.

J. Gao, “Stochastic optimal control of DC pension funds”, Insurance 42 (2008) 1159.

P. Battocchio & F. Menoncin, “Optimal pension management in a stochastic framework”, Insurance 34 (2004) 79.

A. J. G. Cairns, D. Blake & K. Dowd, “Stochastic lifestyling: optimal dynamic asset allocation for defined contribution pension plans”, Journal of Economic Dynamics & Control 30 (2006) 843.

C. Zhang & X Rong, “Optimal investment strategies for DC pension with a stochastic salary under affine interest rate model”. Hindawi Publishing Corporation, 2013 (2013) http://dx.doi.org/10.1155/2013/297875

E. E. Akpanibah , B. O. Osu, K. N. C. Njoku & E. O. Akak, “Optimization of Wealth Investment Strategies for a DC Pension Fund with Stochastic Salary and Extra Contributions”, International Journal of Partial Differential Equations and Application 5 (2017) 33.

K.N. C Njoku, B. O. Osu, E. E. Akpanibah & R. N. Ujumadu, “Effect of Extra Contribution on Stochastic Optimal Investment Strategies for DC Pension with Stochastic Salary under the Ane Interest Rate Model”, Journal of Mathematical Finance 7 (2017) 821.

Y. He & P. Chen, “Optimal Investment Strategy under the CEV Model with Stochastic Interest Rate”, Mathematical Problems in Engineering 2020 (2020) 1

Published

2020-08-01

How to Cite

Portfolio Strategy for an Investor with Logarithm Utility and Stochastic Interest Rate under Constant Elasticity of Variance Model. (2020). Journal of the Nigerian Society of Physical Sciences, 2(3), 186-196. https://doi.org/10.46481/jnsps.2020.86

Issue

Volume 2, Issue 3, August 2020

Section

Original Research
Copyright & Licensing

How to Cite

Portfolio Strategy for an Investor with Logarithm Utility and Stochastic Interest Rate under Constant Elasticity of Variance Model. (2020). Journal of the Nigerian Society of Physical Sciences, 2(3), 186-196. https://doi.org/10.46481/jnsps.2020.86