Strong Convergence Theorems for Split Common Fixed Point Problem of Bregman Generalized Asymptotically Nonexpansive Mappings in Banach Spaces
Keywords:
Split common fixed point problem, Bregman distance, Generalized asymptotically nonexpansive mapping, Strong convergenceAbstract
In this paper, a new iterative scheme is introduced and also strong convergence theorems for solving split common fixed point problem for uniformly continuous Bregman generalized asymptotically nonexpansive mappings in uniformly convex and uniformly smooth Banach spaces are presented. The results are proved without the assumption of semicompactness property and or Opial condition
Dimensions
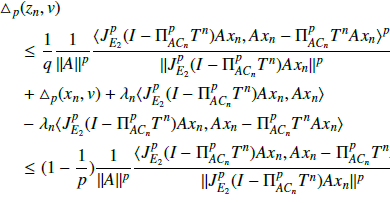
Published
2024-03-06
How to Cite
Strong Convergence Theorems for Split Common Fixed Point Problem of Bregman Generalized Asymptotically Nonexpansive Mappings in Banach Spaces. (2024). Journal of the Nigerian Society of Physical Sciences, 1(2), 35-50. https://doi.org/10.46481/jnsps.2019.9
Issue
Section
Original Research
Copyright & Licensing
Copyright (c) 2019 Journal of the Nigerian Society of Physical Sciences
This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Strong Convergence Theorems for Split Common Fixed Point Problem of Bregman Generalized Asymptotically Nonexpansive Mappings in Banach Spaces. (2024). Journal of the Nigerian Society of Physical Sciences, 1(2), 35-50. https://doi.org/10.46481/jnsps.2019.9
