An Examination of a Second Order Numerical Method for Solving Initial Value Problems

Authors

  • S. E. Fadugba Department of Mathematics, Ekiti State University, Ado Ekiti, Ekiti State
  • S. N. Ogunyebi Department of Mathematics, Ekiti State University, Ado Ekiti, Ekiti State
  • B. O. Falodun Department of Mathematics, University of Ilorin, Kwara State

Keywords:

Accuracy, exact solution, initial value problem, stability

Abstract

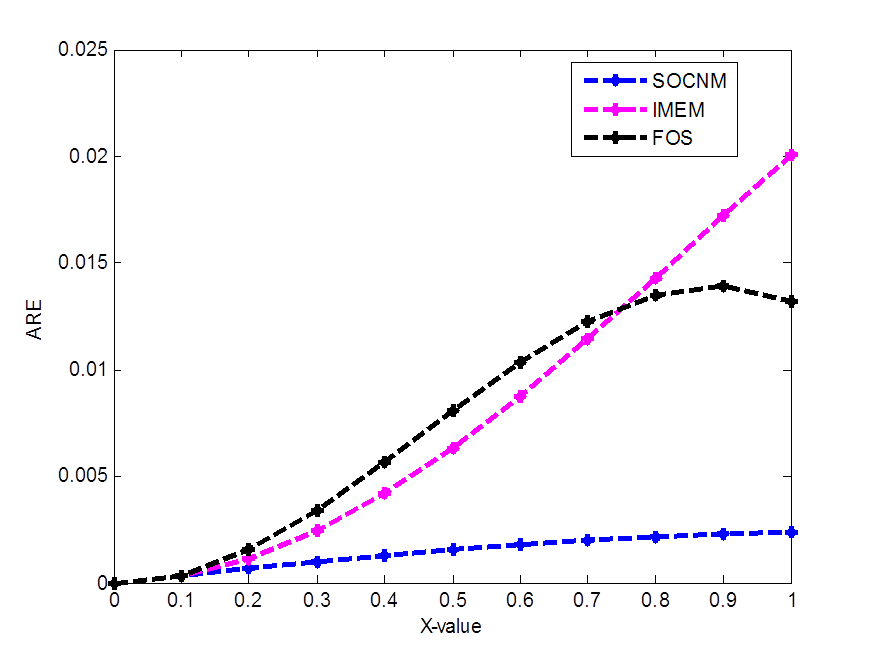
This paper presents an examination of a Second Order Convergence Numerical Method (SOCNM) for solving Initial Value Problems (IVPs) in Ordinary Differential Equations (ODEs). The SOCNM has been derived via the interpolating function comprises of polynomial and exponential forms. The analysis and the properties of SOCNM were discussed. Three numerical examples have been solved successfully to examine the performance of SOCNM in terms of accuracy and stability. The comparative study of SOCNM, Improved Modified Euler Method (IMEM), Fadugba and Olaosebikan Scheme (FOS) and the Exact Solution (ES) is presented. By varying the step length, the absolute relative errors at the final nodal point of the associated integration interval are computed. Furthermore, the analysis of the properties of SOCNM shows that the method is consistent, stable, convergent and has second order accuracy. Moreover, the numerical results show that SOCNM is more accurate than IMEM and FOS and also compared favourably with the ES. By varying the step length, there are two-order decrease in the values of the final absolute relative errors generated via SOCNM. Hence, SOCNM is found to be accurate, stable and a good tool for the numerical solutions of IVPs of different characteristics in ODEs.

Dimensions

S. Fadugba & B. Falodun, “Development of a new one-step scheme for the solution of initial value problem (IVP) in ordinary differential equations”, International Journal of Theoretical and Applied Mathematics, 3 (2017) 58.

N. Ahmad, S. Charan & V. P. Singh, “Study of numerical accuracy of Runge-Kutta second, third and fourth-order method”, International Journal of Computer and Mathematical Sciences, 4 (2015) 111.

S. E. Fadugba & J. O. Idowu, “Analysis of the properties of a third order convergence numerical method derived via transcendental function of exponential form”, International Journal of Applied Mathematics and Theoretical Physics, 5 (2019) 97.

Md. A. Islam, “Accurate solutions of initial value problems for ordinary differential equations with fourth order Runge Kutta method”, Journal of Mathematics Research, 7 (2015) 41.

Md. A. Islam, “A comparative study on numerical solutions of initial value problems (IVP) for ordinary differential equations (ODE) with Euler and Runge Kutta methods”, American Journal of Computational Mathematics 5 (2015) 393.

Y. Ansari, A. Shaikh & S. Qureshi, “Error bounds for a numerical scheme with reduced slope evaluations”, J. Appl. Environ. Biol. Sci. 8 (2018) 67.

J. C. Butcher, Numerical methods for ordinary differential equations, 3rd Edition, John Wiley & Sons, Chichester, West Sussex, 2016.

M. E. Davis, Numerical methods and modeling for chemical engineers, Courier Corporation, New York, 2013.

S. E. Fadugba & J. T. Okunlola, “Performance measure of a new one-step numerical technique via interpolating function for the solution of initial value problem of first order differential equation”, World Scientific News 90 (2017) 77.

S. E. Fadugba & A. O. Ajayi, “Comparative study of a new scheme and some existing methods for the solution of initial value problems in ordinary differential equations”, International Journal of Engineering and Future Technology, 14 (2017) 47.

J. D. Lambert, Numerical methods for ordinary differential systems: the initial value problem, John Wiley & Sons, Inc., New York, 1991.

S. Fadugba & S. Qureshi, “Convergent numerical method using transcendental function of exponential type to solve continuous dynamical systems”, Punjab University Journal of Mathematics, 51 (2019) 45.

O. Abraham, “Improving the modified Euler method”, Leonardo J. Sci. 10 (2007) 1.

S. E. Fadugba & T. E. Olaosebikan, “Comparative study of a class of one-step methods for the numerical solution of some initial value problems in ordinary differential equations”, Research Journal of Mathematics and Computer Science 2 (2018) 1.

J. D. Lambert, Computational methods in ordinary differential equations, John Wiley & Sons Inc., 1973.

J. D. Lambert, Numerical methods for ordinary differential systems: the initial value problem, John Wiley & Sons, Inc., New York, 1991.

Published

2020-08-01

How to Cite

An Examination of a Second Order Numerical Method for Solving Initial Value Problems. (2020). Journal of the Nigerian Society of Physical Sciences, 2(3), 120-127. https://doi.org/10.46481/jnsps.2020.92

Issue

Volume 2, Issue 3, August 2020

Section

Original Research
Copyright & Licensing

How to Cite

An Examination of a Second Order Numerical Method for Solving Initial Value Problems. (2020). Journal of the Nigerian Society of Physical Sciences, 2(3), 120-127. https://doi.org/10.46481/jnsps.2020.92