The Use of Differential Forms to Linearize a Class of Geodesic Equations

Authors

  • J. M. Orverem Department of Mathematical Sciences, Abubakar Tafawa Balewa University Bauchi, Bauchi State, Nigeria; Department of Mathematical Sciences, Federal University Dutsin-Ma, Katsina State, Nigeria
  • Y. Haruna Department of Mathematical Sciences, Abubakar Tafawa Balewa University Bauchi, Bauchi State, Nigeria
  • B. M. Abdulhamid Department of Mathematical Sciences, Abubakar Tafawa Balewa University Bauchi, Bauchi State, Nigeria
  • M. Y. Adamu Department of Mathematical Sciences, Abubakar Tafawa Balewa University Bauchi, Bauchi State, Nigeria

Keywords:

Differential Forms, Linearization, Geodesics Equations, Ordinary Differential Equations, Second Order

Abstract

Lie was the first to consider linearization of differential equations many years ago. Since then, a great deal of research has been done on linearization of differential equations using various methodologies. Surprisingly, there has not been much progress in linearizing geodesic differential equations. In particular, the use of differential forms to linearize a class of geodesic equations is not documented in the literature. Differential forms are used to linearize a class of geodesic differential equations in this research. Geodesics on a plane, geodesics on a cone, and geodesics on a sphere are examples. The solutions to these equations were discovered during the linearization process, as the findings of this study are distinctive, innovative, and original.

Dimensions

H. A. Hamo & I. Sakalli, “Exact solutions to the geodesic equations of linear dilaton black holes”, Turkish Journal of Physics 40 (2016) 139, https://doi.org/10.3906/fiz-1504-4.

W. W. S. Chen, “On finding geodesic equation of two parameters logistic distribution”, Applied Mathematics 6 (2015) 2174.

J. Adamu, A. S. Halliru & B. M. Abdulhamid, “Sciences on some pursuit differential game problem in a Hilbert space”, Journal of the Nigerian Society of Physical Sciences 4 (2022) 379, https://doi.org/10.46481/jnsps.2022.379.

B. Jamil, T. Feroze & M. Safdar, “Optimal systems and their group-invariant solutions to geodesic equations”, International Journal of Geometry Methods in Modern Physics 16 (2019), https://doi.org/10.1142/S0219887819501354.

M. Tsamparlis & A. Paliathanasis, “Lie symmetries of geodesic equations and projective collineations”, Nonlinear Dynamics 62 (2010) 214.

C. Vizman, “Geodesic equations on dif feomorphism groups”, Symmetry, Integrability and Geometry: Methods and Applications 4 (2008) 30.

G. Panou & R. Korakitis, “Geodesic equations and their numerical solutions in geodetic and cartesian coordinates on an oblate spheroid”, Symmetry, Integrability and Geometry: Methods and Applications 4 (2017) 31, https://doi.org/0.1515/jogs-2017-0004.

A. Qadir, “Geometric linearization of ordinary differential equations”, Symmetry, Integrability and Geometry: Methods and Applications (SIGMA) 3 (2007) 103, https://doi.org/10.3842/SIGMA.2007.103.

M. Cariglia, T. Houri, P. Krtou?s & D. Kubiz?n´ak, “On integrability of the geodesic deviation equation”, European Physical Journal C 78 (2018) 661, https://doi.org/10.1140/epjc/s10052-018-6133-1.

F. O. Obarhua & O. J. Adegboro, “An order four continuous numerical method for solving general second order ordinary differential equations”, Journal of the Nigerian Society of Physical Sciences 3 (2021) 150,

https://doi.org/110.46481/jnsps.2021.150.

J. M. Orverem, R. K. Tyokyaa & H. M. Balami, “Differential forms: a tool for linearizing second order ordinary differential equations”, Journal of Scientific and Engineering Research 4 (2017) 10.

B. K. Harrison, “An old problem newly treated with differential forms : when and how can the equation y = f ( x , y , y ) be linearized ?”, Proceedings of Institute of Mathematics of NAS of Ukraine 43 (2002) 2.

J. M. Orverem, Y. Haruna, B. M. Abdulhamid & M. Y. Adamu, “Applying differential forms and the generalized sundman transformations in linearizing the equation of motion of a free particle in a space of constant curvature”, Journal of Mathematics Research 13 (2021) 5, https://doi.org/110.5539/jmr.v13n5p5.

M. T. Mustafa, A. Y. Al-Dweik & R. A. Mara’beh, “On the linearization of second-order ordinary di erential equations to the laguerre form via generalized Sundman transformations”, Symmetry, Integrability

and Geometry: Methods and Applications (SIGMA) 9 (2013) 41, https://doi.org/10.3842/SIGMA.2013.041.

G. W. Bluman & S. C. Anco, Symmetry and integration methods for differential equations, Springer 154 (2004) 430.

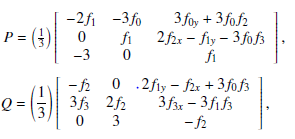
Published

2022-10-08

How to Cite

The Use of Differential Forms to Linearize a Class of Geodesic Equations. (2022). Journal of the Nigerian Society of Physical Sciences, 4(4), 957. https://doi.org/10.46481/jnsps.2022.957

Issue

Volume 4, Issue 4, November 2022

Section

Original Research
Copyright & Licensing

Copyright (c) 2022 J. M. Orverem, Y. Haruna, B. M. Abdulhamid, M. Y. Adamu

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

The Use of Differential Forms to Linearize a Class of Geodesic Equations. (2022). Journal of the Nigerian Society of Physical Sciences, 4(4), 957. https://doi.org/10.46481/jnsps.2022.957