Modelling the transmission dynamics of Omicron variant of COVID-19 in densely populated city of Lagos in Nigeria

Authors

  • Bolarinwa Bolaji Mathematical Sciences department, Prince Abubakar Audu University, Anyigba; Nigeria | Laboratory of Mathematical Epidemiology and Applied Sciences, Prince Abubakar Audu University, Anyigba; Nigeria
  • B. I. Omede Mathematical Sciences department, Prince Abubakar Audu University, Anyigba; Nigeria | Laboratory of Mathematical Epidemiology and Applied Sciences, Prince Abubakar Audu University, Anyigba; Nigeria
  • U. B. Odionyenma Mathematics department, Federal University of Technology, Owerri, Nigeria
  • P. B. Ojih Mathematical Sciences department, Prince Abubakar Audu University, Anyigba; Nigeria
  • Abdullahi A. Ibrahim Mathematical Sciences department, Baze University, Abuja; Nigeria

Keywords:

Epidemiological model, deterministic model

Abstract

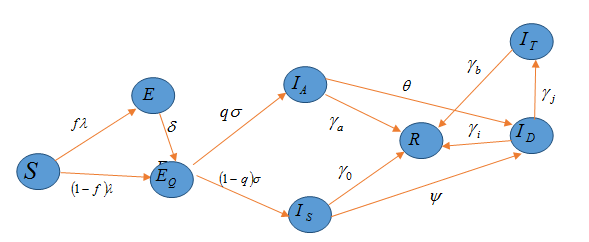
The kernel of the work in this article is the proposition of a model to examine the effect of control measures on the transmission dynamics of Omicron variant of coronavirus disease in the densely populated metropolis of Lagos. Data as relate to the pandemic was gathered as officially released by the Nigerian authority. We make use of this available data of the disease from 1st of December, 2021 to 20th of January, 2022 when omicron variant was first discovered in Nigeria. We computed the basic reproduction number, an epidemiological threshold useful for bringing the disease under check in the aforementioned geographical region of the country. Furthermore, a forecasting tool was derived, for making forecasts for the cumulative number of cases of infection as reported and the number of individuals where the Omicron variant of COVID-19 infection is active for the deadly disease. We carried out numerical simulations of the model using the available data so gathered to show the effects of non-pharmaceutical control measures such as adherence to common social distancing among individuals while in public space, regular use of face masks, personal hygiene using hand sanitizers and periodic washing of hands with soap and pharmaceutical control measures, case detecting via contact tracing occasioning clinical testing of exposed individuals, on the spread of Omicron variant of COVID-19 in the city. The results from the numerical simulations revealed that if detection rate for the infected people can be increased, with majority of the population adequately complying with the safety protocols strictly, then there will be a remarkable reduction in the number of people being afflicted by the scourge of the highly communicable disease in the city.

Dimensions

H. A. Rothana, S. N. Byrareddy, “The epidemiology and pathogenesis of coronavirus disease (COVID-19) outbreak”, J. Auto. Immune. 109 (2020) 102433.

H. Lu, “Drug treatment options for the 2019-new coronavirus 2019nCoV”, Biosci. Trends 14 (2020) 69.

M. Bassetti, A. Vena, D. R. Giacobbe, “The novel chinese coronavirus (2019-nCoV) infections: challenges for fighting the storm”, Eur. J. Clin. Invest. 50 (2020) e13209.

The European Centre for disease prevention and control. Assessed on 7th April 2020 https://www.ecdc.europa.eu/en

The Nigeria Centre for Disease Control. Assessed on 7th April 2020. https://covid19.ncdc.gov.ng

D. Okuonghae and A. Omame, “Analysis of a mathematical model for COVID-19 population dynamics in Lagos, Nigeria”, Chaos, Solitons and Fractals. 139 (2020) 110032.

Y. Bai, L.Yao, T. Wei, F. Tian, D. Y. Jin, L. Chen, M. Wang, “Presumed asymptomatic carrier transmission of COVID-19”, JAMA. 323 (2020) 1406.

A. K. Muhammad, A. Atangana, “Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative”, Alexandria Engineering Journal 59 (2020) 2379.

Tian-Mu Chen, Jia Rui, Qiu-Peng Wang, Ze-Yu Zhao, Jing-An Cui and Ling Yin, “A mathematical model for simulating the phase-based transmissibility of a novel coronavirus”, Infectious Diseases of Poverty 9 (2020) 1.

Coronavirus: the world in lockdown in maps and charts. Assessed on 7th April 2020. https://www.bbc.com/news/world-52103747s

D. Okuonghae, “Lyapunov functions and global properties of some tuberculosis models”, J. Appl. Math. Comput. 48 (2015) 421.

N. Sene, G. Srivastava, “Generalized Mittag-Leffler input stability of the fractional differential equations”, Symmetry 11 (2019) 11050608.

R. A. Umana, A. Omame, S. C. Inyama, “Deterministic and stochastic models of the dynamics of drug resistant tuberculosis”, FUTO J. Ser. 2(2) (2016) 173.

S. A. Ayuba, I. Akeyede & A. Olagunju, “Stability and Sensitivity Analysis of Dengue-Malaria Co-Infection Model in Endemic Stage”, Journal of the Nigerian Society of Physical Sciences 3 (2021) 96. https://doi.org/10.46481/jnsps.2021.196.

F. Y. Eguda, A. James & S. Babuba, “The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method”, Journal of the Nigerian Society of Physical Sciences 1 (2019) 82. https://doi.org/10.46481/jnsps.2019.18.

F. Brauer, C. Castillo-Chavez, A. Mubayi, S. Towers, “Some models for epidemics of vector-transmitted diseases”, Infect. Dis. Model. 1 (2016) 78.

S. Cauchemez, C. Fraser, M. D. Van Kerkhove, C. A. Donnelly, S. Riley, A. Rambaut, “Middle east respiratory syndrome coronavirus: quantification of the extent of the Epidemic, surveillance biases, and transmissibility”, Lancet Infect. Dis. 14 (2014) 50.

M. A. Khan, A. Atangana, “Modeling the dynamics of novel coronavirus 2019-nCoV with fractional derivative”, Alexandria Eng. J. 59 (2020) 2379.

S. O. Sowole, A. A. Ibrahim, D. Sangare, 1. O. Ibrahim, & F. I. Johnson, “Understanding the Early Evolution of COVID-19 Disease Spread using Mathematical Model and MachineLearning Approaches”, Glob. J. Sci. Front. Res. F Math. Decis. Sci (2020) 19.

J. Waku, K. Oshinubi, & J. Demongeot, “Maximal reproduction number estimation andidentification of transmission rate from the first inflection point of new infectious caseswaves: COVID-19 outbreak example”, Mathematics and Computers in Simulations 198 (2022) 47.

N. Crokidakis, “COVID-19 Spreading in Rio de Janeiro, Brazil: do the policies of social isolation really work?”, Chaos Solitons Fractals 136 (2020) 109930.

H. W. Hethcote, “The mathematics of infectious diseases”, SIAM Rev. 42(4) (2000) 599.

L. Xue, S. Jing, J. C. Miller, W. Sun, H. Li, J. G. Estrada-Franco, J. M. Hyman, H. A. Zhu, “Data-driven network model for the emerging COVID-19 epidemics in Wuhan, Toronto and Italy”, Math. Biosci. 326 (2020) 108391.

A. Yousefpour, H. Jahanshahi, S. Bekiros, “Optimal policies for control of the novel Coronavirus disease (COVID-19) outbreak”, Chaos Solitons Fractals 136 (2020) 109883.

J. Adam, T. W. Kucharski, W. Russell, Charlie Diamond, Yang Liu, John Edmunds, Sebastian Funk, M. Rosalind Eggo, “Early dynamics of transmission and control of COVID-19: A mathematical modelling study”, Lancet Infect. Dis. 20 (2020) 553.

I. Aslan, M. Demir, M. G. Wise, S. Lenhart, “Modeling COVID-19: forecasting and analyzing the dynamics of the outbreak in Hubei and Turkey” (2020).

A. Atangana, “Modelling the spread of COVID-19 with new fractalfractional operators: can the lockdown save mankind before vaccination”, Chaos Solitons Fractals 136 (2020) 109860.

N. M. Ferguson, D. Laydon, G. Nedjati-Gilani, N. Imai, K. Ainslie, M. Baguelin, S. Bhatia, A. Boonyasiri, Z. Cucunuba, G. Cuomo-¨ Dannenburg, “Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand”, Imperial College COVID-19 Response Team, London. 16 (2020).

J. Hellewell, S. Abbott, A. Gimma, N. I. Bosse, C. I. Jarvis, T. W. Russell, J. D. Munday, A. J. Kucharski, W. J. Edmunds, F. Sun, “Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts”, Lancet Global Health (2020).

B. Ivorra, M. R. Ferrandez, M. Vela-Perez, A. M. Ramos, “Mathematical modelling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections: The case of China Community”, Nonlinear Sci. Numer. Simulat. (2020).

A. J. Kucharski, T. W. Russell, C. Diamond, Y. Liu, J. Edmunds, S. Funk, “Early dynamics of transmission and control of COVID-19: A mathematical modelling study”, Lancet Infect. Dis. (2020).

K. Mizumoto, H. Chowell, “Transmission potential of the novel coronavirus (COVID-19) on board the diamond princess cruises ship”, Infect. Dis. Model (2020).

E. Shim, A. Tariq, W. Choi, Y. Lee, G. Chowell, “Transmission potential and severity of COVID-19 in South Korea”, Int. J. Infect. Dis. (2020).

Y. Chayu and Jin Wang, “A mathematical model for the novel coronavirus epidemic in Wuhan, China. Mathematical Bioscience and Engineering”, 17(3) (2020) 2708.

P. van den Driessche, J. Watmough, “Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission”, Math. Biosci. 180 (2002) 29.

T. B. Gashirai, S. D. Musekwa-Hove, P. O. Lolika, S. Mushayabasa, “Global stability and optimal control analysis of a foot-and-mouth disease model with vaccine failure and environmental transmission”, Chaos Solitons Fractals 132 (2020) 109568.

J. La Salle, S. Lefschetz, “The stability of dynamical systems. Philadelphia”, SIAM (1976).

T. House, J. V. Ross, D. Sirl, “How big is an outbreak likely to be? Methods for epidemic final-size calculation”, Proc. R. Soc. A. 469 (2013) 20120436. http://dx.doi.org/10.1098/rspa.2012.0436

A. Julien, F. Brauer, P. Van den Driessche, J. Watmough, J. Wu, “A final size relation for epidemic models”, J. Mathematical Biosciences and Engineering 4(2) (2007) 159.

A. B. Gumel, E. A. Iboi, C. N. Ngonghala, & E. H. Elbasha, “A primer on using mathematics to understand COVID-19 dynamics: Modelling, analysis and simulations”, Infectious Disease Modelling (2020), doi: https://doi.org/10.1016/j.idm.2020.11.005

S. M. Blower, H. Dowlatabadi, “Sensitivity and uncertainty analysis of complex models of disease transmission: an HIV model, as an example”, Int. Stat. Rev. 2 (1994) 229.

T-M. Chen, J. Rui, Q-P. Wang, Z-Y. Zhao, J-A. Cui, L. Yin, “A mathematical model for simulating the phase-based transmissibility of a novel coronavirus”, Infect. Dis. Pov 9 (2020) 24.

B. Tang, N. L. Bragazzi, Q. Li, S. Tang, Y. Xiao, J. Wu, ‘’An updated estimation of the risk of transmission of the novel coronavirus (2019nCoV)”, Infect. Dis. Model 5 (2020) 225.

J. McCall, ‘’Genetic algorithms for modelling and optimisation”, J. Comput. Appl. Math. 184 (2005) 205.

Published

2023-04-17

How to Cite

Modelling the transmission dynamics of Omicron variant of COVID-19 in densely populated city of Lagos in Nigeria. (2023). Journal of the Nigerian Society of Physical Sciences, 5(2), 1055. https://doi.org/10.46481/jnsps.2023.1055

Issue

Volume 5, Issue 2, May 2023

Section

Original Research
Copyright & Licensing

Copyright (c) 2023 Bolarinwa Bolaji, B. I. Omede, U. B. Odionyenma, P. B. Ojih, Abdullahi A. Ibrahim

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Modelling the transmission dynamics of Omicron variant of COVID-19 in densely populated city of Lagos in Nigeria. (2023). Journal of the Nigerian Society of Physical Sciences, 5(2), 1055. https://doi.org/10.46481/jnsps.2023.1055