Approximate solution of space fractional order diffusion equations by Gegenbauer collocation and compact finite difference scheme

Solution of space fractional diffusion equation

Authors

  • K. Issa Department of Mathematics and Statistics, Kwara State University, Malete, Kwara State, Nigeria.
  • A. S. Olorunnisola Department of Mathematics and Statistics, Kwara State University, Malete, Kwara State, Nigeria.
  • O. T. Aliu Department of Mathematics and Statistics, Kwara State University, Malete, Kwara State, Nigeria.
  • A. D. Adeshola Department of Mathematics and Statistics, Kwara State University, Malete, Kwara State, Nigeria.

Keywords:

Caputo derivative, fractional diffusion equation, Gegenbauer polynomial, Compact finite difference method (CFDM)

Abstract

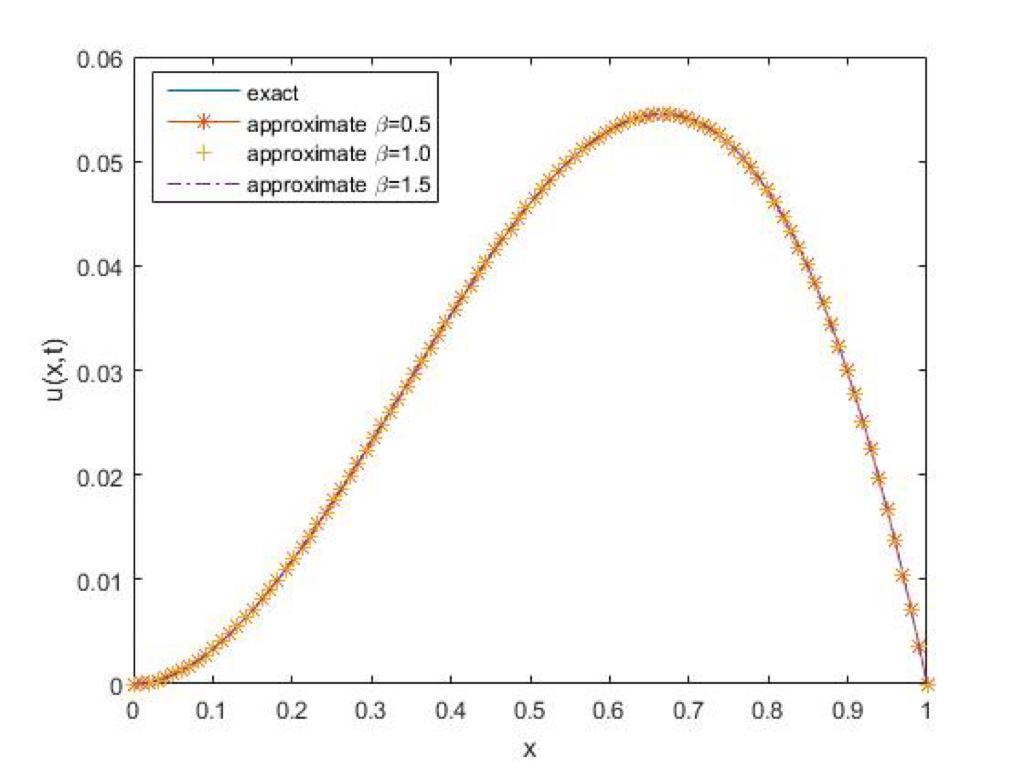
In this paper, approximation of space fractional order diffusion equation are considered using compact finite difference technique to discretize the time derivative, which was then approximated via shifted Gegenbauer polynomials using zeros of (N - 1) degree shifted Gegenbauer polynomial as collocation points. The important feature in this approach is that it reduces the problems to algebraic linear system of equations together with the boundary conditions gives (N + 1) linear equations. Some theorems are given to establish the convergence and the stability of the proposed method. To validate the efficiency and the accuracy of the method, obtained results are compared with the existing results in the literature. The graphical representation are also displayed for various values of \beta Gegenbauer polynomials. It can be observe in the tables of the results and figures that the proposed method performs better than the existing one in the literature.

Dimensions

J. T. Machado, V. Kiryakova & F. Mainardi, “Recent history of fractional calculus”, Commun. Nonlinear Sci. Numer. Simul. 16 (2011) 1140.

A. E. Abouelrega, S. Yao & H. Ahmad, “Analysis of a functionally graded thermopiezoelectric finite rod excited by a moving heat source”, Results in Physics 19 (2020) 103389.

A. Atangana & J. Gómez-Aguilar. “Fractional derivatives with no-index law property: application to chaos and statistics”, Chaos Solitons Fractals 114 (2018) 516.

A. A. Hamoud & K. P. Ghadle, “Some new existence, uniqueness and convergence results for fractional volterra-fredholm integro-differential equations”, J. Appl. Comput. Mech. 5 (2019) 58.

M. Dehghan & A. Saadatmandi, “Chebyshev finite difference method for Fredholm integro-differential equation”, International Journal of Computer Mathematics 85 (2008) 123.

V. O. Bohaienko, “A fast finite-difference algorithm for solving space-fractional filtration equation with a generalised Caputo derivative”, Computational and Applied Mathematics 38 (2019) 1.

K. Issa, B. M. Yisa & J. Biazar, “Numerical solution of space fractional diffusion equation using shifted Gegenbauer polynomials”, Computational Methods for Differential Equations 10 (2022) 431.

A. Saadatmandi & M. Dehghan, “A tau approach for solution of the space fractional diffusion equation”, Computers & Mathematics with Applications 62 (2011) 1135.

N. H. Sweilam, A. M. Nagy & A. A. El-Sayed, “Second kind shifted Chebyshev polynomials for solving space fractional order diffusion equation”, Chaos, Solitons & Fractals, 73 (2015) 141.

H. Hassani, J. T. Machado & E. Naraghirad, “Generalized shifted Chebyshev polynomials for fractional optimal control problems”, Communications in Nonlinear Science and Numerical Simulation 75 (2019) 50.

J. Singh, D. Kumar & D. Baleanu, “New aspects of fractional Biswas-Milovic model with Mittag-Leffler law”, Mathematical Modelling of Natural Phenomena 14 (2019) 303.

K. M. Owolabi & A. Atangana, “High-order solvers for space-fractional differential equations with Riesz derivative”, Discrete & Continuous Dynamical Systems-S 12 (2019) 567.

O. Nikan, A. Golbabai, J. A. Machado, & T. Nikazad, “Numerical solution of the fractional Rayleigh-Stokes model arising in a heated generalized second-grade fluid”, Engineering with Computers, 37 (2021) 1751.

P. Pandey & J. F. Gömez-Aguilar, “On solution of a class of nonlinear variable order fractional reaction-diffusion equation with Mittag-Leffler kernel”, Numer. Methods Partial Differential Eq. 37 (2021) 998.

Y. Salehi, M. T. Darvishi & W. E. Schiesser, “Numerical solution of space fractional diffusion equation by the method of lines and splines”, Applied Mathematics and Computation 336 (2018) 465.

Z. Soori, & A. Aminataei, “Numerical solution of space fractional diffusion equation by spline method combined with Richardson extrapolation”, Computational and Applied Mathematics 39 (2020) 1.

A. H. Bhrawy, & M. M. Al-Shomrani, “A shifted Legendre spectral method for fractional-order multi-point boundary value problems”, Advances in Difference Equations 2012 (2012) 8.

Y. Luchko1 & M. Yamamoto, “Comparison principles for the time-fractional diffusion equations with the Robin boundary conditions. Part I: Linear equations”, Fract. Calc. Appl. Anal., (2023), http://arxiv.org/abs/2304.07812v1.

L. Qiu, X. Ma & Q. Qin, “A novel meshfree method based on spatiotemporal homogenization functions for one-dimensional fourth-order fractional diffusion wave equations”, Applied Math. Letters 142 (2023) 108657.

F. Muhammad, A. Ali, T. T. Merve, M. A. Muhammad, A. Aqeel, E. M. Emad & S. Y. Ibrahim, “Fractal fractional-order derivative for HIV/AIDS model with Mittag-Leffler kernel”, Alexandria Engineering Journal 61 (2022) 10965.

F. Muhammad, A. Muhammad, A. Ali & A. Aqeel, “Modeling of fractional-order COVID-19 epidemic model with quarantine and social distancing”, Mathematical Method in Applied Sciences 44 (2021) 9334.

Y. E. Aghdam, H. Safdari, Y. Azari, H. Jafari & D. Baleanu, “Numerical investigation of space fractional order diffusion equation by the Chebyshev collocation method of the fourth kind and compact finite difference scheme”, Discrete & Continuous Dynamical Systems-S 14 (2021) 2025.

J. C. Mason & D. C. Handscomb, Chebyshev polynomials, Chapman and Hall, CRC Press, 2003.

W. M. Abd-Elhameed1, & Y. H. Youssri, “Fifth-kind orthonormal Chebyshev polynomial solutions for fractional differential equations”, Comp. Appl. Math. 37 (2018) 2897.

Published

2023-05-22

How to Cite

Approximate solution of space fractional order diffusion equations by Gegenbauer collocation and compact finite difference scheme: Solution of space fractional diffusion equation. (2023). Journal of the Nigerian Society of Physical Sciences, 5(2), 1368. https://doi.org/10.46481/jnsps.2023.1368

Issue

Volume 5, Issue 2, May 2023

Section

Original Research
Copyright & Licensing

Copyright (c) 2023 K. Issa, A. S. Olorunnisola, O. T. Aliu, A. D. Adeshola

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Approximate solution of space fractional order diffusion equations by Gegenbauer collocation and compact finite difference scheme: Solution of space fractional diffusion equation. (2023). Journal of the Nigerian Society of Physical Sciences, 5(2), 1368. https://doi.org/10.46481/jnsps.2023.1368