Approximate analytical solution of fractional-order generalized integro-differential equations via fractional derivative of shifted Vieta-Lucas polynomial

Authors

  • Kazeem Issa Department of Mathematics and Statistics, Kwara State University, Malete, Kwara State, P. M. B. 1530, Ilorin Nigeria.
  • Risikat A. Bello Department of Mathematics and Statistics, Kwara State University, Malete, Kwara State, P. M. B. 1530, Ilorin Nigeria.
  • Usman Jos Abubakar Department of Mathematics, University of Ilorin, P. M. B. 1515, Ilorin Nigeria. https://orcid.org/0000-0002-2079-5731

Keywords:

Vieta-Lucas polynomial, Caputo fractional derivative, Generalized-fractional integro-differential equation, Galerkin method

Abstract

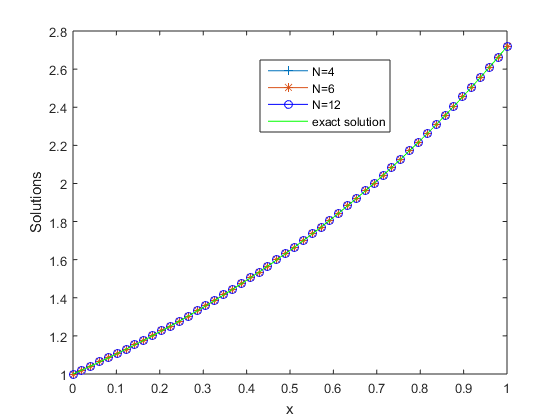
In this paper, we extend fractional-order derivative for the shifted Vieta-Lucas polynomial to generalized-fractional integro-differential equations involving non-local boundary conditions using Galerkin method as transformation technique and obtained N - \delta + 1 system of linear algebraic equations with \lambda i, i = 0, . . . , N unknowns, together with \delta non-local boundary conditions, we obtained (N + 1)- linear equations. The accuracy and effectiveness of the scheme was tested on some selected problems from the literature. Judging from the table of results and figures, we observed that the approximate solution corresponding to the problem that has exact solution in polynomial form gives a closed form solution while problem with non-polynomial exact solution gives better accuracy compared to the existing results.

Dimensions

D. S. Dzhumabaev, “New general solutions to linear Fredholm integro-differential equations and their applications on solving the boundary value problems”, Journal of Computational and Applied Mathematics 327 (2018) 79. https://doi.org/10.1016/j.cam.2017.06.010

K. Issa & F. Salehi, “Approximate solution of perturbed Volterra-Fredholm integrodifferential equations by Chebyshev-Galerkin method”, Journal of Mathematics 2017 (2017) 8213932. https://doi.org/10.1155/2017/8213932

K. Issa, J. Biazar, T. O. Agboola & T. Aliu, “Perturbed Galerkin method for solving integro-differential equations”, Journal of Applied Mathematics 2022 (2022) 9748558. https://doi.org/10.1155/2022/9748558

K. Issa, J. Biazar & B. M. Yisa, “Shifted Chebyshev Approach for the Solution of Delay Fredholm and Volterra Integro-Differential Equations via Perturbed Galerkin Method”, Iranian Journal of Optimization 11 (2019) 149. https://doi.org/20.1001.1.25885723.2019.11.2.8.9

J. Biazar & F. Salehi, “Chebyshev Galerkin method for integro-differential equations of the second kind”, Iranian J. of Numer. Analy. and Opt. 6 (2016) 31. https://doi.org/10.22067/IJNAO.V6I1.37480

H. M. Srivastava, W. Adel, M. Izadi & A. A. El-Sayed, “Solving Some Physics Problems Involving Fractional-Order Differential Equations with the Morgan-Voyce Polynomials. Fractal Fract. 7 (2023) 301. https://doi.org/10.3390/fractalfract7040301

C. Ionescu & J. F. Kelly, “Fractional Calculus for Respiratory Mechanics: Power Law Impedance, Viscoelas-ticity and Tissue Heterogeneity”, Chaos Solitons Fractals 102(2017) 433. https://doi.org/10.1016/j.chaos.2017.03.054

S. Ghosh, “An analytical approach for the fractional-order Hepatitis B model using new operator”, International Journal of Biomathematics 17 (2024) 2350008. https://doi.org/10.1142/S1793524523500080

S. Ghosh & S. Kumar, “Numerical solutions of fractional Covid-19 model using spectral collocation method”, Science & Technology Asia 26 (2021) 2350008. https://doi.org/10.14456/scitechasia.2021.61

M. Jani, D. Bhatta & S. Javadi, “Numerical solution of fractional integro-differential equations with non-local conditions”, Applic. & Appl. Math. 12 (2017) 98. https://digitalcommons.pvamu.edu/aam/vol12/iss1/7/

M. A. Zaky, “An improved tau method for the multi-dimensional fractional Rayleigh?Stokes problem for a heated generalized second grade fluid”, Comput. Math. Appl. 75 (2018) 2243. https://doi.org/10.1016/j.camwa.2017.12.004

Y. Wang & L. Zhu, “Solving nonlinear Volterra integro-differential equations of fractional order by using Euler wavelet method”, Adv. Differ. Equ. 27 (2017) 1. DOI10.1186/s13662-017-1085-6

L. Huang, X. Li, Y. Zhao & X. Duan, “Approximate solution of fractional integro-differential equations by Taylor expansion method”, Comput. & Math. Appl. 62 (2011) 1127. https://doi.org/10.1016/j.camwa.2011.03.037

D. V. Bayram & A. Daşciog̈lu, “A method for fractional Volterra integro-differential equations by Laguerre polynomials”, Adv. Differ. Equ. 2018 (2018) 466. https://doi.org/10.1186/s13662-018-1924-0

A. Daşciog̈lu & D. V. Bayram: Solving Fractional Fredholm Integro-Differential Equations by Laguerre Polynomials. Sains Malaysiana 48 (2019) 251. http://dx.doi.org/10.17576/jsm-2019-4801-29

R. C. Mittal & R. Nigam, “Solution of fractional integro-differential equations by Adomian decomposition method”, Int. J. Adv. Appl. Math. Mech. 4 (2008) 87. http://ijamm.bc.cityu.edu.hk/ijamm/outbox/Y2008V4N2P87C78295535.pdf

Y. Yang, Y. Chen, & Y. Huang, “Convergence analysis of the Jacobi spectral-collocation method for fractional integro-differential equations”, Acta Math. Sci. Ser. B Engl. Ed. 34 (2014) 673. https://doi.org/10.1016/S0252-9602(14)60039-4

X. Ma & C. Huang, “Spectral collocation method for linear fractional integro-differential equations. Applied Mathematical Modelling”, 38 (2014) 1434. https://doi.org/10.1016/j.apm.2013.08.013

M. Yi, L. Wang & J. Huang, “Legendre wavelets method for the numerical solution of fractional integro-differential equations with weakly singular kernel”, Applied Mathematical Modelling 40 (2016) 3422. https://doi.org/10.1016/j.apm.2015.10.009

A. Pedas, E. Tamme & M. Vikerpuur, “Spline collocation for fractional weakly singular integro-differential equations”, Applied Numerical Mathematics 110 (2016) 204. https://doi.org/10.1016/j.apnum.2016.07.011

F. Hendi & M. Al-Qarni, “The variational Adomian decomposition method for solving nonlinear two-dimensional Volterra-Fredholm integro-differential equation”, Journal of King Saud University-Science 31 (2019) 110. https://doi.org/10.1016/j.jksus.2017.07.006

J. H. He, M. H. Taha, M. A. Ramadan & G. M. Moatimid, “A Combination of Bernstein and Improved Block-Pulse Functions for Solving a System of Linear Fredholm Integral Equations”, Math. Probl. Eng. 2022 (2022) 6870751. https://doi.org/10.1155/2022/6870751

J. H. He, M. H. Taha, M. A. Ramadan & G. M. Moatimid, “Improved Block-Pulse Functions for Numerical Solution of Mixed Volterra-Fredholm Integral Equations”, Axioms 10 (2021) 200. https://doi.org/10.3390/axioms10030200

S. Sharma, R. K. Pandey & K. Kumar, “Collocation method with convergence for generalized fractional integro-differential equations”, Journal of Computational and Applied Mathematics 342 (2018) 419. https://doi.org/10.1016/j.cam.2018.04.033

V. Turut, “Numerical comparisons for solving fractional order integro-differential equations with non-local boundary conditions”, Thermal Science 26(2022) 507. https://doi.org/10.2298/TSCI22S2507T

A. A. Hamoud & K. P. Ghadle’ “Modified Laplace decomposition method for fractional Volterra-Fredholm integro-differential equations”, Journal of Mathematical Modeling 6 (2018) 91. DOI:10.22124/JMM.2018.2826

A. Gupta & R. K. Pandey, “Adaptive huber scheme for weakly singular fractional integro-differential equations”, Differential Equations and Dynamical Systems 28 (2020) 527. https://doi.org/10.1007/s12591-020-00516-w

A. I. Fairbairn & M. A. Kelmanson, “Error analysis of a spectrally accurate Volterra-transformation method for solving 1D Fredholm integro-differential equations”, International Journal of Mechanical Sciences 144 (2018) 382. https://doi.org/10.1016/j.ijmecsci.2018.04.052

J. Wang, K. A. Jamal & X. Li, “Numerical Solution of Fractional-Order Fredholm Integro-differential Equation in the Sense of Atangana-Baleanu Derivative”, Mathematical Problems in Engineering 2021 (2021) 6662808. https://doi.org/10.1155/2021/6662808

A. Toma & O. Postavaru, “A numerical method to solve fractional Fredholm-Volterra integro-differential equations”, Alexandria Engineering Journal 68 (2023) 469. https://doi.org/10.1016/j.aej.2023.01.033

G. Szegö, Orthogonal Polynomials, 4th Ed., AMS Colloq. Publ., 1975. https://books.google.com.ng/books?id=ZOhmnsXlcY0C

M. Petkovsek, H. S. Wilf & D. Zeilberger, A=B, A. K. Peters/CRC Press, New York, 1996, pp. 61. https://doi.org/10.1201/9781439864500.

J. C. Mason & D. C. Handscomb, Chebyshev polynomials, Chapman and Hall, CRC Press, 2003. https://doi.org/10.1201/9781420036114

N. H. Sweilam, A. M. Nagy & A. A. El-Sayed, “Second kind shifted Chebyshev polynomials for solving space fractional order diffusion equation”, Chaos, Solitons & Fractals 73 (2015) 141. https://doi.org/10.1016/j.chaos.2015.01.010

K. Issa, A. S. Olorunnisola, T. O. Aliu & A. D. Adeshola, “Approximate solution of space fractional order diffusion equations by Gegenbauer collocation and compact finite difference scheme”, J. Nig. Soc. Phys. Sci. 5 (2023) 1368. https://doi.org/10.46481/jnsps.2023.1368

M. M. Izadkhah and J. Saberi-Nadjafi, “Gegenbauer spectral method for time-fractional convection-diffusion equations with variable coefficients”, Mathematical Methods in the Applied Sc. 38 (2015) 3183. https://doi.org/10.1002/mma.3289

K. Issa, B. M. Yisa & J. Biazar, “Numerical solution of space fractional diffusion equation using shifted Gegenbauer polynomials”, Computational Methods for Differential Equations 10 (2022) 431. https://doi.org/10.22034/cmde.2020.42106.1818

P. Agarwal & A. A. El-Sayed, “Vieta-Luca polynomial for solving a fractional-order mathematical physics model”, Adv. in difference Eqs. 2020 (2020) 626. https://doi.org/10.22034/cmde.2020.42106.1818

M. Z. Youssef, M. M. Khader, I. Al-Dayel & W. E. Ahmed, “Solving fractional generalized Fisher-Kolmogorov-Petrovsky-Piskunov’s equation using compact-finite methods together with spectral collocation algorithms”, Journal in Math. 2022 (2022) 1901131. https://doi.org/10.1155/2022/1901131

K. L. Wang & S. Y. Liu, “He’s fractional derivative and its application for fractional Fornberg-Whitham equation”, Thermal science 21 (2017) 2049. https://doi.org/10.2298/TSCI151025054W

J. H. He, “A new fractal derivation”, Therm. Sci. 15 (2011) 145. https://doi.org/10.2298/TSCI11S1145H

Published

2024-03-06

How to Cite

Approximate analytical solution of fractional-order generalized integro-differential equations via fractional derivative of shifted Vieta-Lucas polynomial. (2024). Journal of the Nigerian Society of Physical Sciences, 6(1), 1821. https://doi.org/10.46481/jnsps.2024.1821

Issue

Volume 6, Issue 1, February 2024

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2024 Kazeem Issa, Risikat A. Bello, Usman Jos Abubakar

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Approximate analytical solution of fractional-order generalized integro-differential equations via fractional derivative of shifted Vieta-Lucas polynomial. (2024). Journal of the Nigerian Society of Physical Sciences, 6(1), 1821. https://doi.org/10.46481/jnsps.2024.1821