A class of single-step hybrid block methods with equally spaced points for general third-order ordinary differential equations

Authors

  • Maduabuchi Gabriel Orakwelu School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Pietermaritzburg, South Africa | DSI-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS), South Africa.
  • Olumuyiwa Otegbeye School of Computer Science and Applied Mathematics, Faculty of Science, University of the Witwatersrand, Johannesburg, South Africa
  • Hermane Mambili-Mamboundou School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Pietermaritzburg, South Africa

Keywords:

Third-order, Hybrid block method, Convergence, Initial and boundary value problems

Abstract

This study presents a class of single-step, self-starting hybrid block methods for directly solving general third-order ordinary differential equations (ODEs) without reduction to first order equations. The methods are developed through interpolation and collocation at systematically selected evenly spaced nodes with the aim of boosting the accuracy of the methods. The zero stability, consistency and convergence of the algorithms are established. Scalar and systems of linear and nonlinear ODEs are approximated to test the effectiveness of the schemes, and the results obtained are compared against other methods from the literature. Significantly, the study shows that an increase in the number of intra-step points improves the accuracy of the solutions obtained using the proposed methods.

Dimensions

P. Henrici, Discrete variable methods in ordinary differential equations, Wiley, New York, 1962.

M. Rajabi, F. Ismail & N. Senu “Linear 3 and 5-step methods using Taylor series expansion for solving special 3rd order ODEs”, AIP Conference Proceedings 1739 (2016) 020036. https://doi.org/10.1063/1.4952516.

O. Adeyeye & Z. Omar, “Solving third order ordinary differential equations using one-step block method with four equidistant generalized hybrid points”, IAENG International Journal of Applied Mathematics 49 (2019) 1. https://www.iaeng.org/IJAM/issues v49/issue 2/IJAM 49 215.pdf.

Z. A. Majid, N. A. Azmi, M. Suleiman & Z. B. Ibrahim, “Solving directly general third order ordinary differential equations using two-point four step block method”, Sains Malaysiana 41 (2012) 623. http://www.ukm.edu.my/jsm/pdf files/SM-PDF-41-5-2012/1520Zanariah.pdf.

R. Allogmany & F. Ismail, “Implicit Three-Point Block Numerical Algorithm for Solving Third Order Initial Value Problem Directly with Applications”, Mathematics 8 (2020) 1771. https://doi.org/10.3390/ math8101771.

S. N. Jator, “On the numerical integration of third order boundary value problems by linear multistep methods”, International Journal of Pure and Applied Mathematics 46 (2008) 375. https://www.researchgate.net.

K. Hussain, O. Adeyeye & N. Ahmad,“Numerical Solution of Second Order Fuzzy Ordinary Differential Equations using Two-Step Block Method with Third and Fourth Derivatives”, Journal of the Nigerian Society of Physical Sciences 5 (2023) 1087. https://doi.org/10.46481/jnsps.2023.1087.

O. Adeyeye, A. Aldalbahi, J. Raza, Z. Omar, M. Rahaman, M. RahimiGorji & N. M. Hoang,“Nonlinear solution of the reaction-diffusion equation using a two-step third-fourth derivative block method”, International Journal of Nonlinear Sciences and Numerical Simulation 22 (2021) 111. https://doi.org/10.1515/ijnsns-2019-0309.

D. O. Awoyemi & O. M. Idowu, “A class of hybrid collocation methods for third-order ordinary differential equation”, International Journal of Computer Mathematics 82 (2005) 1287. https://doi.org/10.1080/00207160500112902.

J. Sunday & J. N. Ndam, “An Accuracy-preserving Block Hybrid Algorithm for the Integration of Second-order Physical Systems with Oscillatory Solutions”, Journal of the Nigerian Society of Physical Sciences 5 (2023) 1017. https://doi.org/10.46481/jnsps.2023.1017.

S. N. Jator, T. Okunlola & T. Biala, R. Adeniyi, “Direct integrators for the general third-Order ordinary differential equations with an application to the Korteweg–de Vries Equation”, International Journal of Applied & Computational Mathematics 4 (2018) 1. https://doi.org/10.1007/ s40819-018-0542-6.

S. N. Jator & E. Agyingi, “Block Hybrid-Step Backward Differentiation Formulas for Large Stiff Systems”, International Journal of Computational Mathematics 2014 (2014) 8. https://doi.org/10.1155/2014/162103.

H. Ramos, “An optimized two-step hybrid block method for solving first-order initial value problems in ODEs”, Differential Geometry- Dynamical System 19 (2017) 107. http://vectron.mathem.pub.ro/dgds/v19/ D19-ra-C97P.pdf.

M. G. Orakwelu, S. Goqo & S. Motsa, “An optimized two-step block hybrid method with symmetric intra-step points for second order initial value problems”, Engineering Letters 29 (2021) 948. http://www. engineeringletters.com/issues v29/issue 3/EL 29 3 18.pdf.

U. Mohammed, J. Garba, A. A. Alhaji, A. I. Maali & M. Semenov,´ “Second derivatives single step block hybrid method for nonlinear dynamical systems”, Nigerian Journal of Mathematics and Applications 32 (2022) 42. http://repository.futminna.edu.ng:8080/jspui/handle/ 123456789/19414.

P. Onumanyi, U. W. Sirisena & S. N. Jator, “Continuous finite difference approximation for solving differential equations ”, International Journal of Computer Mathematics 72 (1999) 15. https://doi.org/10.1080/ 00207169908804831.

S. N. Jator, “On a class of hybrid method for y′′ = f(x,y,y′)”, International Journal of Pure and Applied Mathematics 59 (2010) 381. https://doi.org/10.1080/00207169108804026.

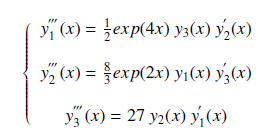
Published

2023-11-28

How to Cite

A class of single-step hybrid block methods with equally spaced points for general third-order ordinary differential equations. (2023). Journal of the Nigerian Society of Physical Sciences, 5(4), 1484. https://doi.org/10.46481/jnsps.2023.1484

Issue

Volume 5, Issue 4, November 2023

Section

Original Research
Copyright & Licensing

Copyright (c) 2023 Maduabuchi Gabriel Orakwelu, Olumuyiwa Otegbeye, Hermane Mambili-Mamboundou

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

A class of single-step hybrid block methods with equally spaced points for general third-order ordinary differential equations. (2023). Journal of the Nigerian Society of Physical Sciences, 5(4), 1484. https://doi.org/10.46481/jnsps.2023.1484