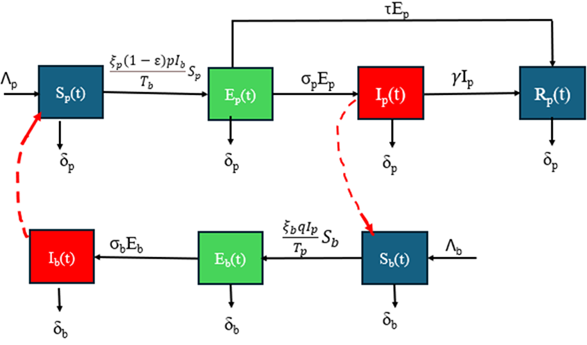
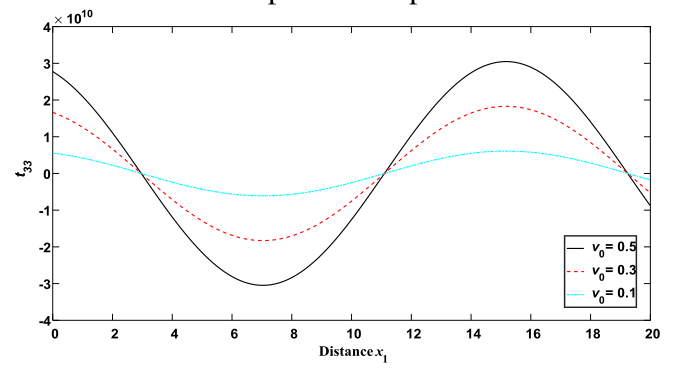
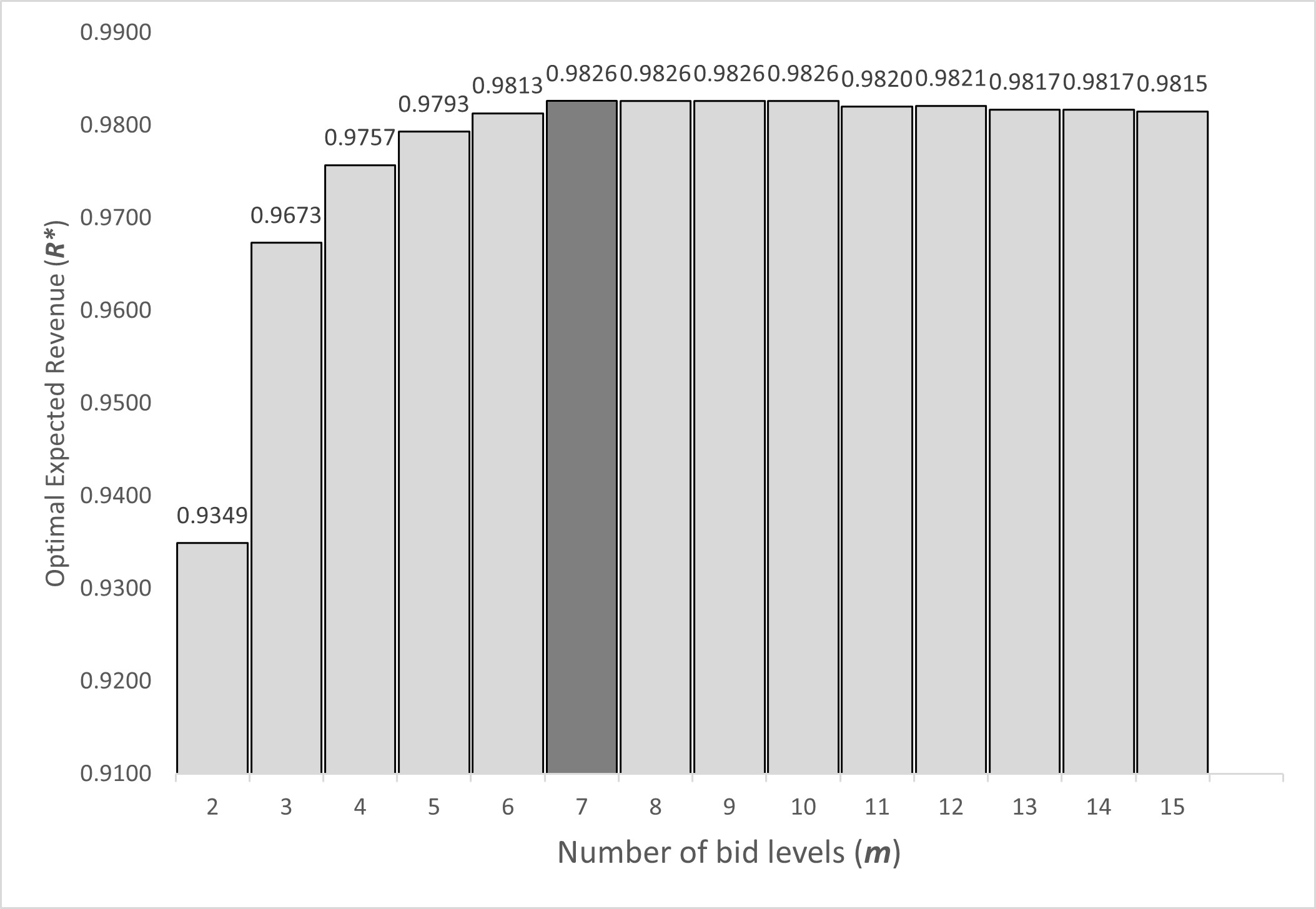
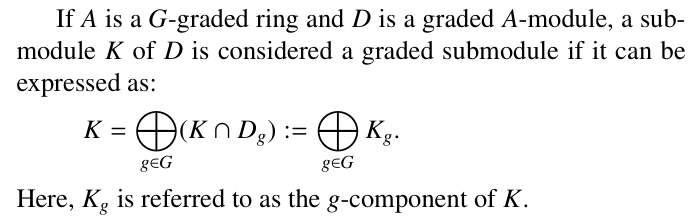Why Publish With JNSPS
We are committed to supporting you throughout your publishing “journey” – from submission, through peer review, to publication and promotion
Open Access
JNSPS is a strong supporter of open access (OA). All the research articles published in JNSPS are fully open access.
Read moreRefereed
Peer review process - Committed to serving the scientific community. JNSPS uses a single-blind peer-review process.
Read moreIndexed
The journal is indexed and abstracted in DOAJ, Crossref, Scopus, Google Scholar, WorldCat, Researchgate, etc.
Read more100,000 NGN
APC is 100,000 NGN as an active Nigerian member of NSPS. Non-member/non-active member of NSPS pays 300 USD or its Naira equivalence
Read more