Differential and fuzzy differential sandwich theorems involving quantum calculus operators

Authors

  • I. R. Silviya School of Advanced Sciences, VIT University, Chennai-600 127, Tamil Nadu, India
  • K. Muthunagai School of Advanced Sciences, VIT University, Chennai-600 127, Tamil Nadu, India

Keywords:

Differential subordination, Differential superordination, q- calculus operators;

Abstract

The principle of subordination is useful in comparing two holomorphic functions when the range of one holomorphic function is a subset of the other and they comply at a single point. The subordination, when spoken in fuzzy set theory, becomes fuzzy subordination as the comparison between two holomorphic functions is made using the fuzzy membership function. In this article, differential and fuzzy differential Subordination, superordination, and sandwich theorems have been discussed for the classes defined by using q-derivative and symmetric q-derivative operators.

Dimensions

E. L. Lindelof, “Memoire sur certaines inegalites dans la theorie des fonctions monogenes et sur quelques proprietes nouvelles de ces fonctions dans le voisinage d’un point singulier essentiel”, Acta Soc. Sci. Fennicae 35 (1909) 3. http://www.zentralblatt-math.org/zmath/en/advanced/?q=an:40.0439.02.

J. E. Littlewood, “On inequalities in the theory of functions”, Proceedings of the London Mathematical Society 2 (1925) 481.

W. Rogosinski, “On subordinate functions”, Mathematical Proceedings of the Cambridge Philosophical Society 35 (1939) 1. https://doi.org/10.1017/S0305004100020703.

D. J. Hallenbeck & S. Ruscheweyh, “Subordination by convex functions”, Proceedings of the American Mathematical Society 52 (1975) 191. https://doi.org/10.2307/2040127.

W. Ma, A unified treatment of some special classes of univalent functions, Proceedings of the Conference on Complex Analysis, International Press Inc., 1992.

G. M. Goluzin, “On the majorization principle in function theory”, Dokl. Akad. Nauk. SSSR 42 (1935) 935.

R. M. Robinson,“ Univalent majorants”, Transactions of the American Mathematical Society 61 (1947) 1. https://doi.org/doi:10.2307/1990287

T. J. Suffridge, “Some remarks on convex maps of the unit disk”, Duke Mathematical Journal 37 (1970) 775. https://doi.org/10.1215/S0012-7094-70-03792-0

S. S. Miller & P. T. Mocanu, “Differential subordinations and univalent functions”, Michigan Mathematical Journal 28 (1981) 157. https://doi.org/10.1307/mmj/1029002507.

S. S Miller & P. T Mocanu, “Subordinants of differential superordinations”, Complex variables 48 (2003) 815. https://doi.org/10.1080/02781070310001599322.

T. Bulboaca,“Classes of first-order differential superordinations”, Demonstratio Mathematica 35 (2002) 287. https://doi.org/10.1515/dema-2002-0209.

T. Bulboaca, “A class of superordination-preserving integral operators”, Indagationes Mathematicae 13 (2002) 301. https://doi.org/10.1016/S0019-3577(02)80013-1.

F. H. Jackson, “on q-functions and a certain difference operator”, Earth and Environmental Science Transactions of the Royal Society of Edinburgh 46 (1909) 253. https://doi.org/10.1017/S0080456800002751.

F. H. Jackson, “On q-definite integrals”, Quart. J. Pure Appl. Math 41.(1910) 193.

H. M. Srivastava, Univalent functions, fractional calculus, and associated generalized hypergeometric functions. In Univalent functions, fractional calculus, and their applications; H. M. Srivastava, S. Owa (Eds.); John Wiley & Sons: New York, USA, 1989.

M. E. H. Ismail, E. Merkes & D. Styer, “A generalization of starlike functions”, Complex Variables, Theory and Application: An International Journal 14 (1990) 77. https://doi.org/10.1080/17476939008814407.

S. Abelman, K. A. Selvakumaran, M. M. Rashidi & S. D. Purohit “Subordination conditions for a class of non-Bazilevic type defined by using fractional q-calculus operators”, Facta Univ. Ser. Math. Inform 32(2017) 255. https://doi.org/10.22190/FUMI1702255A.

S. Agrawal & S. K. Sahoo, “A generalization of starlike functions of order alpha”, Hokkaido Mathematical Journal 46 (2017) 15. https://doi.org/10. 14492/hokmj/1498788094.

M. Govindaraj & S. Sivasubramanian, “On a class of analytic functions related to conic domains involving q-calculus”, Analysis Mathematica 43 (2017) 475. https://doi.org/10.1007/s10476-017-0206-5.

H. M. Srivastava, B. Ahmad, N. Khan, M.G. Khan, W. K. Mashwani & B. Khan, “A subclass of multivalent Janowski type q-starlike functions and its consequences”, Symmetry 13 (2021) 1275. https://doi.org/10.3390/sym13071275.

Q. Z. Ahmad, N. Khan, M. Raza, M. Tahir & B. Khan, “Certain qdifference operators and their applications to the subclass of meromorphic q-starlike functions”, Filomat 33 (2019) 3385. https://doi.org/10.2298/ FIL1911385A.

B. Ahmad, W. K. Mashwani, S. Araci, S. Mustafa, M. G. Khan & B.Khan, “A subclass of meromorphic Janowski-type multivalent qstarlike functions involving a q-differential operator”, Advances in Continuous and Discrete Models 2022 (2022) 1. https://doi.org/10.1186/ s13662-022-03683-y.

L.A. Zadeh, “Fuzzy sets”, Information and control 8 (1965) 338. http://dx.doi.org/10.1016/S0019-9958(65)90241-X.

G. I. Oros & G. Oros, “The notion of subordination in fuzzy sets theory”, General Mathematics 19 (2011) 97. https://generalmathematics.ro/ wp-content/uploads/2020/03/12 Oros.pdf.

G. I. Oros & G. Oros, “Fuzzy differential subordination”, Acta Universitatis Apulensis 30 (2012) 55. http://emis.icm.edu.pl/journals/AUA/acta30/Paper6-Acta30-2012.pdf.

G. I. Oros & G. Oros, “Dominants and best dominants in fuzzy differential subordinations”, Stud. Univ. Babes-Bolyai Math 57 (2012) 239. https://www.cs.ubbcluj.ro/?studia-m/2012-2/13-oros-final.pdf.

W. G. Atshan & K. O. Hussain, “Fuzzy Differential Superordination”, Theory and Applications of Mathematics and Computer Science 7 (2017) 27. https://www.researchgate.net/publication/311518845 Fuzzy differential superordination.

A. K. Wanas & A. H. Majeed, “Fuzzy differential subordination properties of analytic functions involving generalized differential operator”, Sci. Int. (Lahore) 30 (2018) 297.

S. M. El-Deeb & A. A. Lupas, “A. Fuzzy differential subordinations associated with an integral operator”, An. Univ. Oradea Fasc. Mat 27 (2020) 133.

S.M. El-Deeb & G.I Oros, “Fuzzy differential subordinations connected with the linear operator”, Mathematica Bohemica 146 (2021) 397. https://doi.org/10.21136/MB.2020.0159-19.

A.Alb Lupas & A. Catas, “Fuzzy differential subordination of the Atangana-Baleanu fractional integral”, Symmetry 13 (2021) 1929. https://doi.org/10.3390/sym13101929.

G. I. Oros, “New fuzzy differential subordinations”, Communications Faculty of Sciences University of Ankara Series A1 Mathematics and Statistics 70 (2021) 229. https://doi.org/10.31801/cfsuasmas.784080.

A. Alb Lupas, “Applications of the fractional calculus in fuzzy differential subordinations and superordinations”, Mathematics 9 (2021) 2601. https: //doi.org/10.3390/math9202601.

A. Kareem, “Fuzzy differential subordinations for analytic functions involving Wanas operator and some applications in fractional calculus”, Ikonion Journal of Mathematics 2 (2020) 1. https://dergipark.org.tr/en/pub/ikjm/issue/56257/653379.

B. Khan, Z. G. Liu, T.G. Shaba, S .Araci, N. Khan & M.G Khan, “Applications of q-derivative operator to the subclass of bi-univalent functions involving-Chebyshev polynomials”, Journal of Mathematics 2022 (2022) 1. https://doi.org/10.1155/2022/8162182.

S. Altinkaya, S. Kanas & S. Yal, “Subclass of k-uniformly starlike functions defined by symmetric q-derivative operator”, Ukrains kyi Matematychnyi Zhurnal 70 (2018) 1499. https://doi.org/10.1007/s11253-019-01602-1.

S. Khan, S. Hussain, M. Naeem, M. Darus & A. Rasheed, “A subclass of q-starlike functions defined by using a symmetric q-derivative operator and related with generalized symmetric conic domains”, Mathematics 9 (2021) 917. https://doi.org/10.3390/math9090917.

V. O. Atabo & S. O. Adee, “A new special 15-step block method for solving general fourth order ordinary differential equations”, Journal of the Nigerian society of Physical Sciences 3 (2021) 308. https://doi.org/10.46481/jnsps.2021.337.

A. Thirumalai, K. Muthunagai & Ritu Agarwal “Pre-functions and Extended pre-functions of Complex Variables”, Journal of the Nigerian Society of Physical Sciences 5 (2023) 1427.https://doi.org/10.46481/jnsps.2023.1427.

A.M.C.B. da Cruz & N. Martins, “The q-symmetric variational calculus”, Computers and Mathematics with Applications 64 64 (2012) 2241. https://doi.org/10.1016/j.camwa.2012.01.076.

A. Lavagno, “Basic-deformed quantum mechanics”, Reports on Mathematical Physics 64 (2009) 79. https://doi.org/10.1016/S0034-4877(09)90021-0

S. S. Miller & P. T. Mocanu, Differenatial subordinations theory and applications, Marcel Dekker Inc., New York, 2000.

E. A. Haydar, “On fuzzy differential subordination”, Mathematica Moravica 19 (2015) 123. https://scindeks.ceon.rs/Article.aspx?artid= 1450-59321501123H.

1832

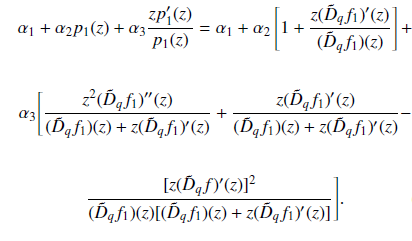
Published

2024-03-06

How to Cite

Differential and fuzzy differential sandwich theorems involving quantum calculus operators. (2024). Journal of the Nigerian Society of Physical Sciences, 6(1), 1832. https://doi.org/10.46481/jnsps.2024.1832

Issue

Volume 6, Issue 1, February 2024

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2023 I. R. Silviya, K. Muthunagai

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Differential and fuzzy differential sandwich theorems involving quantum calculus operators. (2024). Journal of the Nigerian Society of Physical Sciences, 6(1), 1832. https://doi.org/10.46481/jnsps.2024.1832