Iterative method for the numerical solution of optimal control model for mosquito and insecticide

Authors

  • S. Adamu Department of Mathematics, Nigerian Army University Biu, Borno State, Nigeria https://orcid.org/0000-0003-1690-4269
  • O. O. Aduroja Department of Mathematics, University of Ilesa, Ilesa, Osun State, Nigeria
  • A. S. Onanaye Department of Mathematics, Redeemer’s University, Ede, Osun State, Nigeria
  • M. R. Odekunle Department of Mathematics, Modibbo Adama University Yola, Adamawa State, Nigeria

Keywords:

Malaria, mosquito, insecti, First Boubaker polynomials, optimal control problems, mathematical models

Abstract

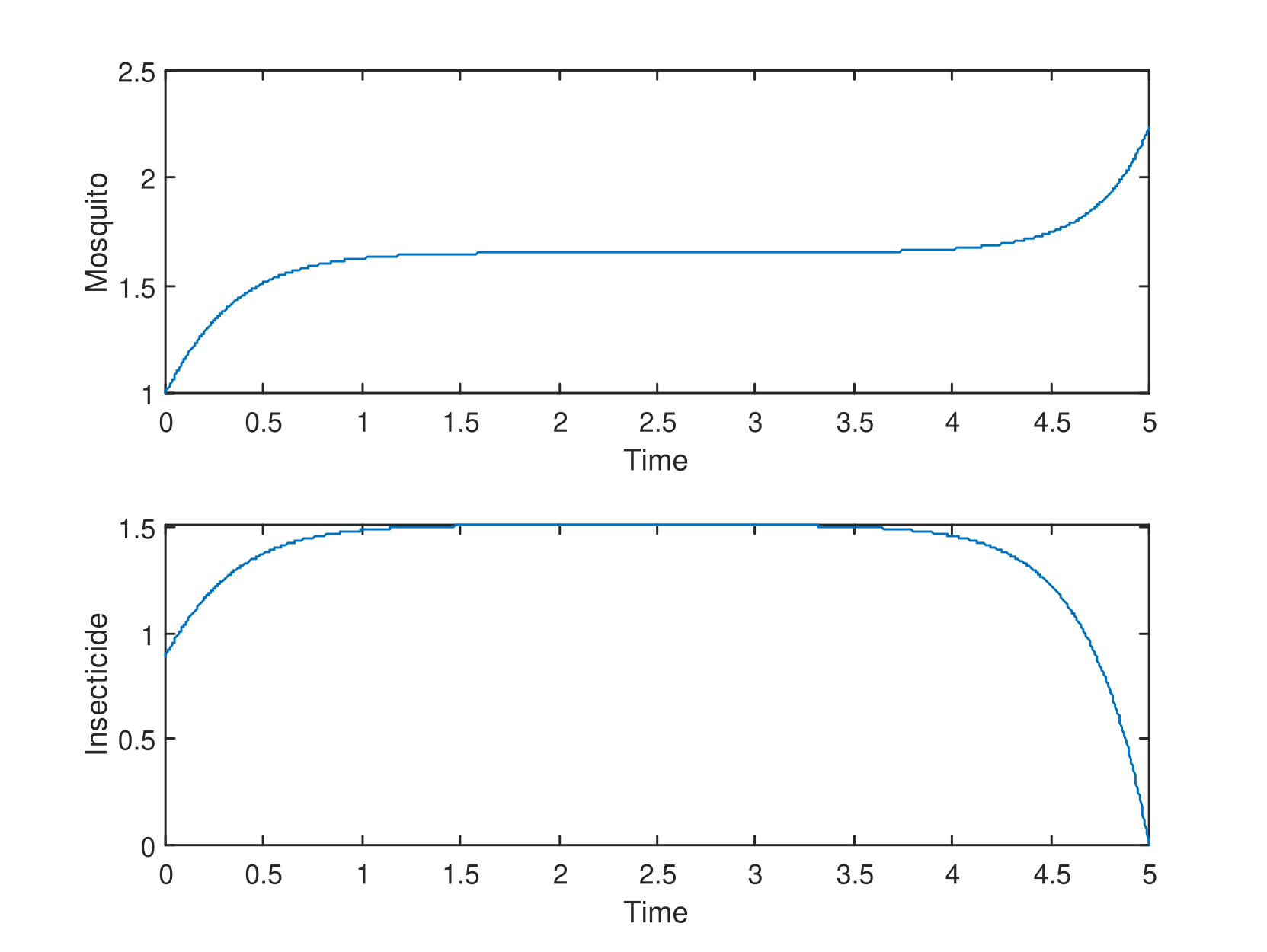
A linear multistep method is transformed into an iterative method based on Patade and Bhalekar's technique for the numerical solution of the optimal control problem modeled for mosquito and insecticide management using forward-backward sweep methods via Pontryagin's principle. Stability and convergence analysis of the iterative method are carried out, and it is found to be stable, convergent, and of order four. Results obtained by the method clearly show that the population of mosquitoes can be minimized to a large extent using the new iterative method while reducing the harmful effects of the insecticide, subsequently reducing the spread of malaria.

Dimensions

J. Patade & S. Bhalekar, “A new numerical method based on DaftardarGejji and Jafari technique for solving differential equations”, World Journal of Modeling and Simulation 11 (2015) 256. https://www.researchgate.net/publication/283498636_A_new_numerical_method_based_on_Daftardar-Gejji_and_Jafari_Technique_for_solving_differential_equations.

M. Kida, S. Adamu, O. O. Aduroja & T. P. Pantuvo, “Numerical Solution of Stiff and Oscillatory Problems using Third Derivative Trigonometrically Fitted Block Method”, J. Nig. Soc. Phys. Sci. 4 (2022) 34. https://journal.nsps.org.ng/index.php/jnsps/article/view/271.

S. Adamu, K. Bitrus & H. L. Buhari, “One step second derivative method using Chebyshev collocation point for the solution of ordinary differential equations”, J. of NAMP 51 (2019) 47. https://www.researchgate.net/publication/360777358_One_step_second_derivative_method_using_Chebyshev’s_Collocation_Point_for_the_solution_of_Ordinary_Differential_Equations.

A. M. Alkali, M. Ishiyaku, S. Adamu & D. Umar, “Third derivative integrator for the solution of first order initial value problems”, Savannah Journal of Science and Engineering Technology 1 (2023) 300.

https://www.academia.edu/112593436/Third_derivative_integrator_for_the_solution_of_first_order_initial_value_problems?uc-g-sw=94218086.

M. G. Orakwelua, O. Otegbeye & H. Mambili-Mamboundoua, “A class of single-step hybrid block methods with equally spaced points for general third-order ordinary differential equations”, J. Nig. Soc. Phys. Sci. 5 (2023) 1484. https://journal.nsps.org.ng/index.php/jnsps/article/view/1484.

O. O. Olaiya, M. I. Modebeia & S. A. Bello, “A One-Step Block Hybrid Integrator for Solving Fifth Order Korteweg-de Vries Equations”, J. Nig. Soc. Phys. Sci. 4 (2022) 797. https://journal.nsps.org.ng/index.php/jnsps/article/view/797.

A. B. H. Bashir, O. B. E. Hassan & O. A. Almahi, “Modeling optimal control for mosquito and insecticide”, Mathematical Theory and Modeling 10 (2020) 58. https://www.iiste.org/Journals/index.php/MTM/article/view/53653.

A. L. A. Araujo, J. L. Boldrini, R. C. Cabrales, E. Fernandez-Cara & M. L. Oliveira, “Optimal Control of Insect Populations”, Mathematics 9 (2021) 1762. https://www.mdpi.com/2227-7390/9/15/1762.

F. Fatmawati, F. Herdicho, Windarto, W. Chukwu, H. Tasman, “An optimal control of malaria transmission model with mosquito seasonal fac tor”, Results in Physics 25 (2021) 1. https://doi.org/10.1016/j.rinp.2021.104238.

R. R. Garret, Numerical Methods for Solving Optimal Control Problems, Tennessee Research and Creative Exchange, University of Tennessee, Knoxville, 2015. https://trace.tennessee.edu/utk_gradthes/3401/.

S. Adamu, “Numerical Solution of Optimal Control Problems using Block Method”, Electronic Journal of Mathematical Analysis and Applications 11 (2023) 1. https://journals.ekb.eg/article_312691.html.

S. Lenhart & J. T. Workman, Optimal Control Applied to Biological Models. Chapman & Hall/CRC, London New York, 2007. https://www.taylorfrancis.com/books/mono/10.1201/9781420011418/optimal-control-applied-biological-models-suzanne-lenhart-john-workman.

S. Adamu, O. O. Aduroja, & K. Bitrus, “Numerical Solution to Optimal Control Problems using Collocations Method via Pontrygin’s Principle”, FUDMA Journal of Sciences 7 (2023) 228. https://fjs.fudutsinma.edu.ng/index.php/fjs/article/view/2016.

H. Musa, I. Saidu & M. Y. Waziri, “A Simplified Derivation and Analysis of Fourth Order Runge Kutta Method”, International Journal of Computer Applications 9 (2010) 975. https://ijcaonline.com/volume9/number8/pxc3871891.pdf.

F. B. Hildebrand, Introduction to Numerical Analysis: Second Edition, Tata McGraw-Hill Publishing Co. Limited, New Delhi, 1974, pp. 55-8284. https://www.amazon.com/Introduction-Numerical-Analysis-Second-Mathematics/dp/0486653633.

M. R. Odekunle, N. D. Oye & S. O. Adee, “A class of inverse Runge-Kutta schemes for the numerical integration of singular problems”, Applied Mathematics and Computation 158 (2004) 149. https://sciencedirect.com/science/article/abs/pii/S009630030301018X.

T. A. Anake, Continuous Implicit Hybrid One-Step Methods for the solution of Initial Value Problems of General Second Order Ordinary Differential Equations, Ph.D Thesis, Covenant University, Ota, Nigeria, 2011. https://eprints.covenantuniversity.edu.ng/7856/1/CUGP060192Anake%2C%20Timothy%20Ashibel.pdf.

S. Davaeifar & J. Rashidinia, “Boubaker polynomials collocation approach for solving systems of nonlinear Volterra–Fredholm integral equation”, Journal of Taibah University for Science, 11 (2017) 1182. https://www.sciencedirect.com/science/article/pii/S1658365517300638.

J. C. Butcher, “A history of Runge-Kutta Methods”, Applied Numerical Mathematics 20 (1996) 247. https://www.sciencedirect.com/science/article/abs/pii/0168927495001085.

The optimal Mosquito population and Insecticide for case 2.

Published

2024-04-23

How to Cite

Iterative method for the numerical solution of optimal control model for mosquito and insecticide. (2024). Journal of the Nigerian Society of Physical Sciences, 6(2), 1965. https://doi.org/10.46481/jnsps.2024.1965

Issue

Volume 6, Issue 2, May 2024 (In Progress)

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2024 S. Adamu, O. O. Aduroja, A. S. Onanaye, M. R. Odekunle

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Iterative method for the numerical solution of optimal control model for mosquito and insecticide. (2024). Journal of the Nigerian Society of Physical Sciences, 6(2), 1965. https://doi.org/10.46481/jnsps.2024.1965