A new Maxwell-Log logistic distribution and its applications for mortality rate data

Uthumporn  Panitanarak; Aliyu  Ismail Ishaq; Alfred Adewole Abiodun; Hanita  Daud; Ahmad Abubakar Suleiman

doi:10.46481/jnsps.2025.1976

Authors

Uthumporn Panitanarak Department of Biostatistics, Faculty of Public Health, Mahidol University, 10400, Thailand
Aliyu Ismail Ishaq
[email protected]
Department of Statistics, Ahmadu Bello University, Zaria, 810107, Nigeria
Alfred Adewole Abiodun Department of Statistics, University of Ilorin, Ilorin, 240003, Nigeria
Hanita Daud Fundamental and Applied Sciences Department, Universiti Teknologi PETRONAS, Seri Iskandar, 32610, Malaysia
Ahmad Abubakar Suleiman Fundamental and Applied Sciences Department, Universiti Teknologi PETRONAS, Seri Iskandar, 32610, Malaysia

Keywords:

Log-Logistic distribution, Maxwell generalized family, Maxwell-Log Logistic distribution, Order statistics, COVID-19

Abstract

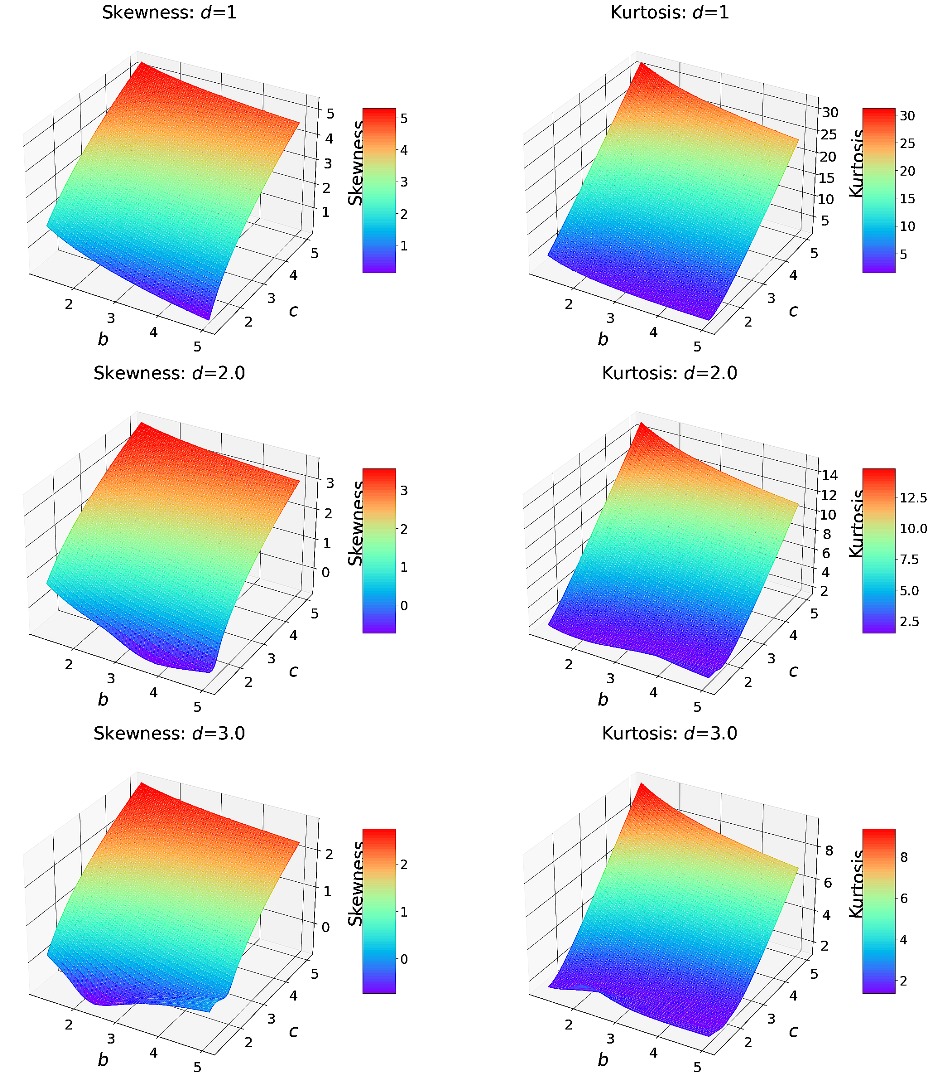
In this research, we extended the Log-Logistic distribution by incorporating it into the Maxwell generalized class, resulting in the Maxwell-Log Logistic (Max-LL ) distribution. The probability density function and cumulative distribution function of the proposed distribution have been defined. The proposed distribution’s density shapes can be left or right-skewed and symmetric. The failure function of this distribution might be increasing, decreasing, or inverted bathtub forms. We discussed some essential properties of the Max-LL distribution, including moments, moment generating function, probability weighted moments, stress-strength, and order statistics. The efficiency of the model parameters has been evaluated through a simulation study utilizing a quantile function. To assess the proposed distribution’s adaptability, we applied it to two lifetime datasets: global COVID-19 mortality rates (for nations with more than 100,000 cases) and Canadian COVID-19 mortality rates. The Maxwell-Log Logistic distribution outperformed other distributions on both datasets, as evidenced by several accuracy measures. This shows that the proposed distribution is the best fit for COVID-19 mortality rate data in Canada and around the world.

Dimensions

REFERENCES

[1] A. I. Ishaq, A. A. Suleiman, A. Usman, H. Daud & R. Sokkalingam, “Transformed Log-Burr III distribution: Structural features and appli cation to milk production”, Engineering Proceedings 56 (2023) 322. https://doi.org/10.3390/ASEC2023-15289.

[2] A. I. Ishaq, A. A. Suleiman, H. Daud, N. S. Sawaran Singh, M. Othman, R. Sokkalingam, P. Wiratchotisatian, A. G. Usman & S. I. Abba, “LogKumaraswamy distribution: its features and applications”, Frontiers in Applied Mathematics and Statistics 9 (2023) 1258961. https://doi.org/10.3389/fams.2023.1258961.

[3] H. Daud, A. A. Suleiman, A. I. Ishaq, N. Alsadat, M. Elgarhy, A. Usman, P. Wiratchotisatian, A. U. Ubale & Y. Liping, “A new extension of the Gumbel distribution with biomedical data analysis”, Journal of Radiation Research and Applied Sciences 17 (2024) 101055. https://doi.org/10.1016/j.jrras.2024.101055.

[4] I. E. Ragab, H. Daud, A. A. Suleiman, N. Alsadat, V. B. Nagarjuna & M. Elgarhy, “Type II Topp-Leone exponentiated gamma distribution with application to breaking stress data”, Journal of Radiation Research and Applied Sciences 17 (2024) 101045. https://doi.org/10.1016/j.jrras.2024.101045.

[5] P. F. Verhulst, “Notice sur la loi que la population suit dans son accroissement”, Correspondence mathematique et physique 10 (1838) 113. https://cir.nii.ac.jp/crid/1570009749935841536.

[6] P. R. Fisk, “The graduation of income distributions,” Econometrica: journal of the econometric society,” 29 (1961) 171. https://www.econometricsociety.org/publications/econometrica/1961/04/01/graduation-income-distributions.

[7] S. Bennett, “Log-logistic regression models for survival data”, Journal of the Royal Statistical Society Series C: Applied Statistics 32 (1983) 165. https://doi.org/10.2307/2347295.

[8] Y. Yu, Y. Jia, M. A. Alshahrani, O. A. Alamri, H. Daud, J. G. Dar & A. A. Suleiman, “Adopting a new sine-induced statistical model and deep learning methods for the empirical exploration of the music and reliability data”, Alexandria Engineering Journal 104 (2024) 396. https://doi.org/10.1016/j.aej.2024.07.104.

[9] P. R. Tadikamalla, “A look at the Burr and related distributions”, International Statistical Review/Revue Internationale de Statistique 48 (1980) 337. https://doi.org/10.2307/1402945.

[10] C. Kleiber & S. Kotz, Statistical size distributions in economics and actuarial sciences, John Wiley & Sons, 2003. https://doi.org/10.1002/0471457175.

[11] J. F. Lawless, Statistical models and methods for lifetime data, John Wiley & Sons, 2011. https://doi.org/10.1002/9781118033005.

[12] R. B. D’Agostino, “Modelling survival data in medical research”, Journal of the American Statistical Association 90 (1995) 1125. https://doi.org/10.1093/jrsssa/qnae038.

[13] M. Ahmad, C. Sinclair & A. Werritty, “Log-logistic flood frequency analysis”, Journal of Hydrology 98 (1988) 205. https://doi.org/10.1016/0022-1694.

[14] N. Balakrishnan and H. Malik, “Best linear unbiased estimation of location and scale parameters of the log-logistic distribution”, Communications in Statistics-Theory and Methods 16 (1987) 3477. https://doi.org/10.1080/03610928708829586.

[15] F. Ashkar & S. Mahdi, “Fitting the log-logistic distribution by generalized moments”, Journal of Hydrology 328 (2006) 694. https://doi.org/10.1016/j.jhydrol.2006.01.014/

[16] T. V. F. De Santana, E. M. Ortega, G. M. Cordeiro & G. O. Silva, “The Kumaraswamy-log-logistic distribution”, Journal of Statistical Theory and Applications 11 (2012) 265. https://www.researchgate.net/publication/316154940_The_Kumaraswamy-Log-Logistic_Distribution.

[17] G. M. Cordeiro & M. De Castro, “A new family of generalized distributions”, Journal of statistical computation and simulation 81 (2011) 883. https://doi.org/https://doi.org/10.1080/00949650903530745.

[18] R. C. Gupta, P. L. Gupta & R. D. Gupta, “Modeling failure time data by Lehman alternatives”, Communications in Statistics-Theory and methods 27 (1988) 887. https://www.tandfonline.com/doi/abs/10.1080/03610929808832134

[19] W. Gui, “Marshall-Olkin extended log-logistic distribution and its application in minification processes”, Applied Mathematical Sciences 7 (2013) 77. http://dx.doi.org/10.12988/ams.2013.35268.

[20] M. H. Tahir, M. Mansoor, M. Zubair & G. Hamedani, “McDonald loglogistic distribution with an application to breast cancer data”, Journal of Statistical Theory and Applications 13 (2014) 65. https://doi.org/10.2991/jsta.2014.13.1.6.

[21] V. Kariuki, A. Wanjoya & O. Ngesa, “Properties, estimation, and applications of the extended log-logistic distribution”, Scientific Reports 14 (2024) 20967. https://doi.org/10.1038/s41598-024-68843-4.

[22] D. C. T. Granzotto & F. Louzada, “The transmuted log-logistic distribution: modeling, inference, and an application to a polled tabapua race time up to first calving data”, Communications in Statistics-Theory and Methods 44 (2015) 3387. http://dx.doi.org/10.1080/03610926.2013.775307.

[23] W. T. Shaw & I. R. Buckley, “The alchemy of probability distributions: beyond Gram-Charlier expansions, and a skew-kurtotic-normal distribution from a rank transmutation map”, arXiv preprint arXiv:0901.0434 (2009). https://doi.org/10.48550/arXiv.0901.0434.

[24] L. D. Ribeiro-Reis, “Unit log-logistic distribution and unit log-logistic regression model”, Journal of the Indian Society for Probability and Statis tics 22 (2021) 375. https://doi.org/10.1007/s41096-021-00109-y.

[25] A. K. Fulment, S. R. Gadde & J. K. Peter, “The odd log-logistic generalized exponential distribution: Application on survival times of chemotherapy patients data”, F1000research 11 (2022). http://dx.doi.org/10.12688/f1000research.127363.1.

[26] R. Hosana, N. W. W. S. Sari & A. Kurniawan, “Survival analysis and hazard of log logistic distribution on type I censored data parametrically”, Contemporary Mathematics and Applications 5 (2023) 79. https://e-journal.unair.ac.id/CONMATHA/article/view/47040.

[27] M. K. Shakhatreh & M. A. Aljarrah, “Bayesian analysis of unit log logistic distribution using non-informative priors”, Mathematics 11 (2023) 4947. https://doi.org/10.3390/math11244947.

[28] V. Ranjbar, A. Eftekharian, O. Kharazmi, and M. Alizadeh, “Odd log logistic generalised Lindley distribution with properties and applications”, Statistics in Transition new series 24 (2023) 71. http://dx.doi.org/10.59170/stattrans-2023-052.

[29] M. C. Santos & R. R. Pescim, “A new extension of the Burr XII distribution generated by odd log-logistic random variables”, Communications in Statistics-Theory and Methods 53 (2024) 5003. https://doi.org/10.1080/03610926.2023.2200560.

[30] Z. Ma, M. Wang & C. Park, “Robust explicit estimation of the log-logistic distribution with applications”, Journal of Statistical Theory and Practice 17 (2023) 21. https://doi.org/10.1007/s42519-023-00322-x.

[31] A. F. Fagbamigbe, G. K. Basele, B. Makubate & B. O. Oluyede, “Application of the exponentiated Log-logistic weibull distribution to censored data”, Journal of the Nigerian Society of Physical Sciences 1 (2019) 12. http://dx.doi.org/10.46481/jnsps.2019.4.

[32] I. E. Okorie, A. C. Akpanta, J. Ohakwe, D. C. Chikezie, C. U. Onyemachi & M. K. Rastogi, “Zero-truncated Poisson-power function distribution”, Annals of Data Science 8 (2021) 107. https://doi.org/10.1007/s40745-019-00201-y.

[33] A. Fayomi, S. Khan, M. H. Tahir, A. Algarni, F. Jamal & R. Abu-Shanab, “A new extended gumbel distribution: Properties and application”, Plos one 17 (2022) e0267142. https://doi.org/10.1371/journal.pone.0267142.

[34] M. Arif, D. M. Khan, M. Aamir, M. El-Morshedy, Z. Ahmad & Z. Khan, “A new flexible exponentiated-x family of distributions: characterizations and applications to lifetime data”, IETE Journal of Research 69 (2022) 1. https://www.tandfonline.com/doi/abs/10.1080/03772063.2022.2034537.

[35] A. Ishaq, A. Usman, M. Tasi’u, A. Suleiman & A. Ahmad, “A new odd f-weibull distribution: properties and application of the monthly Nigerian naira to british pound exchange rate data”, International Conference on Data Analytics for Business and Industry (ICDABI) (2022) 326. https://doi.org/10.1109/ICDABI56818.2022.10041527.

[36] A. A. Suleiman, M. Othman, A. I. Ishaq, M. L. Abdullah, R. Indawati, H. Daud & R. Sokkalingam, “A new statistical model based on the novel generalized odd beta prime family of continuous probability distributions with applications to cancer disease data sets”, (2022). https://doi.org/10.20944/preprints202212.0072.v.

[37] M. Muhammad et al., “A new extension of the topp–leone-family of models with applications to real data”, Annals of Data Science 10 (2023) 225. https://link.springer.com/article/10.1007/s40745-022-00456-y.

[38] G. P. Dhungana & V. Kumar, “Exponentiated Odd Lomax Exponential distribution with application to COVID-19 death cases of Nepal,” PloS one 17 (2022) e0269450. https://doi.org/10.1371/journal.pone.0269450.

[39] A. A. Suleiman, H. Daud, N. S. S. Singh, M. Othman, A. I. Ishaq & R. Sokkalingam, “A novel odd beta prime-logistic distribution: desirable mathematical properties and applications to engineering and environmental data”, Sustainability 15 (2023) 10239. https://doi.org/10.3390/su151310239.

[40] A. I. Ishaq, U. Panitanarak, A. A. Abiodun, A. A Suleiman, & H. Daud, “The generalized odd maxwell-kumaraswamy distribution: its properties and applications”, Contemporary Mathematics, 5 (2024) 711–742. https://doi.org/10.37256/cm.5120242888.

[41] F. Vilca, C. Borelli Zeller & N. Balakrishnan, “Multivariate Birnbaum–Saunders distribution based on a skewed distribution and associated EM-estimation”, Brazilian Journal of Probability and Statistics 37 (2023) 26. https://doi.org/10.1214/22-BJPS559.

[42] M. Kamal et al., “A new improved form of the Lomax model: Its bivariate extension and an application in the financial sector”, Alexandria Engineering Journal 75 (2023) 127. https://doi.org/10.1016/j.aej.2023.05.027.

[43] F. Willayat, N. Saud, M. Ijaz, A. Silvianita & M. El-Morshedy, “Marshall–Olkin Extended Gumbel Type-II distribution: properties and applications”, Complexity 2022 (2022) 2219570. https://onlinelibrary.wiley.com/doi/full/10.1155/2022/2219570.

[44] S. M. Aljeddani & M. Mohammed, “An extensive mathematical approach for wind speed evaluation using inverse Weibull distribution”, Alexandria Engineering Journal 76 (2023) 775. https://doi.org/10.1016/j.aej.2023.06.076.

[45] S. B. Sayibu, A. Luguterah & S. Nasiru, “McDonald Generalized power weibull distribution: properties, and applications”, J. Stat. Appl. Pro. 13 (2024) 297. https://dx.doi.org/10.18576/jsap/130121.

[46] A. A. Suleiman, H. Daud, N. S. S. Singh, A. I. Ishaq & M. Othman, “A new odd beta prime-burr x distribution with applications to petroleum rock sample data and covid-19 mortality rate”, Data 8 (2023) 143. https://doi.org/10.3390/data8090143.

[47] M. Kamal, H. E. Sadig, A. Al Mutairi, I. Alkhairy, F. M. A. Zaghdoun, M. Yusuf, E. Hussam, M. Abotaleb, M. S. Mustafa & A. F. Alsaedy, “A new updated version of the Weibull model with an application to re-injury rate data”, Alexandria Engineering Journal 83 (2023) 92. http://dx.doi.org/10.1016/j.aej.2023.10.018.

[48] A. Usman, A. I. Ishaq, A. A. Suleiman, M. Othman, H. Daud & Y. Aliyu, “Univariate and bivariate log-topp-leone distribution using censored and uncensored datasets”, in Computer Sciences & Mathematics Forum 7 (2023) 32. https://doi.org/10.3390/IOCMA2023-14421.

[49] A. I. Ishaq & A. A. Abiodun, “The Maxwell–Weibull distribution in modeling lifetime datasets”, Annals of Data Science 7 (2020) 639. https://doi.org/10.1007/s40745-020-00288-8

[50] A. Alzaatreh, C. Lee & F. Famoye, “A new method for generating families of continuous distributions”, Metron 71 (2013) 63. https://link.springer.com/article/10.1007/s40300-013-0007-y.

[51] U. A. Abdullahi, A. A. Suleiman, A. I. Ishaq, A. Usman & A. Suleiman,“The Maxwell–exponential distribution: theory and application to life time data”, Journal of Statistical Modeling & Analytics (JOSMA) 3(2021). http://dx.doi.org/10.22452/josma.vol3no2.4.

[52] A. I. Ishaq, A. A. Abiodun & J. Y. Falgore, “Bayesian estimation of the parameter of Maxwell-Mukherjee Islam distribution using assumptions of the Extended Jeffrey’s, Inverse-Rayleigh and Inverse-Nakagami priors under the three loss functions”, Heliyon 7 (2021). https://doi.org/10.1016/j.heliyon.2021.e08200.

[53] A. I. Ishaq & A. A. Abiodun, “On the developments of Maxwell-Dagum distribution”, Journal of Statistical Modelling: Theory and Applications 2 (2021) 1. https://www.researchgate.net/publication/357312489_On_thedevelopments_of_Maxwell-Dagum_distribution.

[54] K. Koobubpha, T. Panitanarak, P. Domthong & U. Panitanarak, “The maxwell-burr X distribution: its properties and applications to the COVID-19 mortality rate in Thailand”, Thailand Statistician 21 (2023) 421. https://ph02.tci-thaijo.org/index.php/thaistat/article/view/249011.

[55] A. A. Suleiman, A. Suleiman, U. A. Abdullahi & A. Suleiman, “Estimation of the case fatality rate of COVID-19 epidemiological data in Nigeria using statistical regression analysis”, Biosafety and Health 3 (2021) 4. https://doi.org/10.1016/j.bsheal.2020.09.003.

[56] A. A. Osi, M. Abdu, U. Muhammad, A. Ibrahim, L.A. Isma’il, A. A. Suleiman, H. S. Abdulkadir, S. S. Sada, H. G. Dikko & M. Z. Ringim, “A classification approach for predicting COVID-19 Patient’s survival outcome with machine learning techniques”, MedRxiv (2020). http://dx.doi.org/10.5455/sf.aaosi2.

[57] P. Samui, J. Mondal & S. Khajanchi, “A mathematical model for COVID 19 transmission dynamics with a case study of India”, Chaos, Solitons & Fractals 140 (2020) 110173. https://doi.org/10.1016/j.chaos.2020.110173.

[58] T. Rocha Filho et al., “A data-driven model for COVID-19 pandemic–Evolution of the attack rate and prognosis for Brazil”, Chaos, Solitons & Fractals 152 (2021) 111359. https://doi.org/10.1016/j.chaos.2021.111359.

[59] B. H. Foy, B. Wahl, K. Mehta, A. Shet, G. I. Menon & C. Britto, “Comparing COVID-19 vaccine allocation strategies in India: A mathematical modelling study”, International Journal of Infectious Diseases 103 (2021) 431. https://doi.org/10.1016/j.ijid.2020.12.075

[60] A. A. Suleiman, H. Daud, A. I. Ishaq, M. Othman, H. M. Alshanbari & S. N. Alaziz, “A novel extended Kumaraswamy distribution and its application to COVID-19 data”, Engineering Reports 6 (2024) e12967. https://doi.org/10.1002/eng2.12967.

[61] I. S. Gradshteyn & I. M. Ryzhik, Table of integrals, series, and products”, Academic press, 2014. https://doi.org/10.1016/C2010-0-64839-5.

[62] J. A. Greenwood, J. M. Landwehr, N. C. Matalas & J. R. Wallis, “Probability weighted moments: definition and relation to parameters of several distributions expressable in inverse form”, Water resources research 15 (1979) 1049. https://doi.org/10.1029/WR015i005p01049.

[63] S. Dey, T. Dey, S. Ali & M. S. Mulekar, “Two-parameter Maxwell distribution: Properties and different methods of estimation”, Journal ofStatistical Theory and Practice 10 (2026) 291. https://doi.org/10.1080/15598608.2015.1135090.

[64] S. Ali, S. Dey, M. Tahir & M. Mansoor, “A comparison of different methods of estimation for the flexible Weibull distribution”, Communications Faculty of Sciences University of Ankara Series A1 Mathematics and Statistics 69 (2020) 794. https://doi.org/10.1214/22-BJPS546.

[65] S. Ali, J. Ara & I. Shah, “A comparison of different parameter estimation methods for exponentially modified Gaussian distribution”, Afrika Matematika 33 (2022) 58. https://doi.org/10.1007/s13370-022-00995-w.

[66] M. Alizadeh, A. Z. Afify, M. S. Eliwa & S. Ali, “The odd log-logistic Lindley-G family of distributions: properties, Bayesian and non-Bayesian estimation with applications”, Computational statistics 35 (2020) 281. https://doi.org/10.1007/s00180-019-00932-9.

[67] S. Ali, S. Dey, M. H. Tahir & M. Mansoor, “Two-parameter logistic exponential distribution: Some new properties and estimation methods”, American Journal of Mathematical and Management Sciences 39 (9) (20202). https://doi.org/10.1080/01966324.2020.1728453.

[68] E. M. Almetwally, R. Alharbi, D. Alnagar & E. H. Hafez, “A new inverted topp-leone distribution: applications to the COVID-19 mortality rate in two different countries”, Axioms 10 (2021) 25. https://doi.org/10.3390/axioms10010025.

[69] K. Rosaiah, R. Kantam & S. Kumar, “Reliability test plans for exponentiated log-logistic distribution”, Stochastics and Quality Control 21 (2006) 279. https://doi.org/10.1515/EQC.2006.2792006.