A ninth-order first derivative method for numerical integration

Authors

  • Richard O. Akinola Department of Mathematics, University of Jos, Jos, Plateau State, Nigeria
  • Ezekiel O. Omole Mathematics Programme, Department of Physical Sciences, Landmark University, Omu–Aran, Kwara State, Nigeria
  • Joshua Sunday Department of Mathematics, University of Jos, Jos, Plateau State, Nigeria
  • Stephen Y. Kutchin Department of Mathematics, University of Jos, Jos, Plateau State, Nigeria

Keywords:

Non–singular, A(α)–stable, Stiffness, Convergence

Abstract

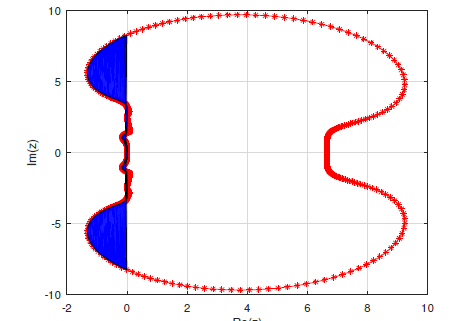
In this paper, we present a ninth–order block hybrid method for the numerical solution of stiff and non–stiff systems of first–order differential equations. The method is based on an interpolation and collocation approach which results in a single continuous formulation; from which eight discrete schemes that make the block method were obtained. A convergence analysis of our method illustrated that it is A–stable, consistent, and convergent. We applied our method to some numerical examples which showed that the new method not only outperformed a second derivative method of order fourteen in the literature but also compared well with the exact solution.

Dimensions

F. Iavernaro & F. Mazzia, “Convergence and stability of multistep methods solving nonlinear initial value problems”, SIAM Journal on Scientific Computing 18 (1997) 270. https://doi.org/10.1137/S1064827595287122.

G. Kirlinger, “Linear multistep methods applied to stiff initial value problems-a survey”, Mathematical and Computer Modelling 40 (2004) 1181. https://doi.org/10.1016/j.mcm.2005.01.012.

G. Albi, M. Herty & L. Pareschi, ”Linear multistep methods for optimal control problems and applications to hyperbolic relaxation systems”, Applied Mathematics and Computation 354 (2019) 460. https://doi.org/10.1016/j.amc.2019.02.021.

J. D. Lambert, Computational methods in ordinary differential equations, John Wiley, New York, 1973. https://doi.org/10.1002/zamm.19740540726.

P. Oliver, “A family of linear multistep methods for the solution of stiff and non-stiff ODEs”, IMA Journal of Numerical Analysis 2 (1982) 289. https://doi.org/10.1093/imanum/2.3.289.

J. C. Butcher, Numerical methods for ordinary differential equations, John Wiley and Sons Ltd, New Jersey, 2016. https://onlinelibrary.wiley.com/doi/book/10.1002/9781119121534.

J. C. Butcher, “Numerical methods for ODE in the 20th century”, Journal of Computational and Applied Mathematics 125 (2000) 1. https://doi.org/10.1016/S0377-0427(00)00455-6.

E. O. Omole & L. A. Ukpebor, “A step by step guide on derivation and analysis of a new numerical method for solving fourth-order ODE”, Mathematics Letters 6 (2020) 13. https://doi.org/10.11648/j.ml.20200602.12.

W. B. Gragg & H. J. Stetter, “Generalized multistep predictor?corrector methods”, J. ACM 11 (1964) 188. http://doi.org/10.1145/321217.321223.

J. C. Butcher, “A multistep generalization of Runge-?Kutta method with four or five stages”, J. Ass. Comput 14 (1967) 84. https://dl.acm.org/doi/pdf/10.1145/321371.321378.

M. Urabe, “An implicit one?step method of high?order accuracy for the numerical integration of ODE”, J. Numer. Math. 15 (1970) 151. https://link.springer.com/article/10.1007/BF02165379#citeas.

T. A. Mitsui, “Modified version of Urabe’s implicit single?step method”, J. Comp. Appli. Math. 20 (1987) 325. https://doi.org/10.1016/0377-0427(87)90149-X.

R. O. Akinola & K. J. Ajibade, “A Proof of the Non-Singularity of the D Matrix Used in Deriving the two–Step Butcher’s Hybrid Scheme for the Solution of Initial Value Problems”, Journal of Applied Mathematics and Physics 9 (2021) 3177. https://doi.org/10.4236/jamp.2021.912208.

N. M. Kamoh, D. G. Gyemang & M. C. Soomiyol, “On one justification on the use of hybrids for the solution of first order initial value problems of ODE”, Pure and Applied Mathematics Journal 6 (2017) 137. https://doi.org/10.11648/j.pamj.20170605.11.

T. Aboiyar, T. Luga & B. V. Iyorter, “Derivation of Continuous Linear Multistep Methods Using Hermite Polynomials as Basis Functions”, American Journal of Applied Mathematics and Statistics 3 (2015) 220. https://doi.org//:10.12691/ajams-3-6-2.

A. U. Fotta, T. J. Alabi & B. Abdulqadir, “Block method with one hybrid point for the solution of first order initial value problems of ODE”, International Journal of Pure and Applied Mathematics 103 (2015) 511. http://dx.doi.org/10.12732/ijpam.v103i3.12.

S. O. Ayinde, E. A. Ibijola. “A New Numerical Method for Solving First Order Differential Equations”, American Journal of Applied Mathematics and Statistics 3 (2015) 156. https://doi.org/10.12691/ajams-3-4-4.

S. A. Odejide & A. O. Adeniran, “A hybrid linear collocation multistep scheme for solving first order initial value problems”, Journal of the Nigerian Mathematical Society 31 (2012) 229. https://ojs.ictp.it/jnms/index.php/jnms/article/view/764.

R. O. Akinola, A. Shokri, S. W. Yao & S. Y. Kutchin, “Circumventing ill-conditioning arising from using linear multistep methods in approximating the solution of initial value problems”, Mathematics 10 (2022) 2910. https://doi.org/10.3390/math10162910.

N. I. N. Ismail, Z. A. Majid & N. Senu, “Solving neutral delay differential equation of pantograph type”, Malaysian Journal of Mathematical Sciences 14 (2020) 107. https://einspem.upm.edu.my/journal/fullpaper/vol14sdec/8.%20Nur%20Inshirah.pdf.

N. I. N. Ismail, Z. A. Majid & N. Senu, “Hybrid multistep block method for solving neutral delay differential equations”, Sains Malaysiana 49 (2020) 929. http://doi.org/10.17576/jsm-2020-4904-22.

A. Kherd, Z. Omar, A. Saaban & O. Adeyeye, “Solving first and second order delay differential equations using new operational matrices of Said–Ball polynomials”, Journal of Interdisciplinary Mathematics 24 (2021) 921. http://doi.org/10.1080/09720502.2020.1850994.

K. Hussain, O. Adeyeye, N. Ahmad, “Solving First Order Nonlinear Fuzzy Initial Value Problems Using Two Step Block Method with Presence of Higher Derivatives”, AIUB journal of Science and Engineering (AJSE) 22 (2023) 112. http://doi.org/10.53799/ajse.v22i2.337

D. G. Yakubu, A. Shokri, G. M. Kumleng & D. Marian, “Second derivative block hybrid methods for the the numerical integration of differential systems”, Fractal Fract. 6 (2022) 386. https://doi.org/10.3390/fractalfract6070386.

P. Onumanyi, D. O. Awoyemi, S. N. Jator & U. W. Sirisena, “New linear multistep methods with continuous coefficients for first order initial value problems”, Journal of Nigerian Mathematics Society 13 (1994) 37. https://www.scirp.org/reference/referencespapers?referenceid=2699834.

P. Kaps, S. W. H. Poon &T. D. Bui, “Rosenbrock methods for stiff ODEs: A comparison of Richardson extrapolation and embedding technique”, Computing 34 (1985) 17. https://link.springer.com/article/10.1007/BF02242171#citeas.

W. H. Enright, “Second derivative multistep methods for stiff ODE”, SIAM J. Numer. Anal. 11 (1974) 321. https://www.jstor.org/stable/2156073.

W. C. Gear, “DIFSUB for Solution of ODE”, Comm. ACM. 14 (1971) 185. https://dl.acm.org/doi/10.1145/362566.362573.

C. W. Alan, “ODEPACK, A systematized collection of ODE solvers”, in Scientific Computing, R. S. Stepleman (Ed.), Lawrence Livermore National Laboratory, Livermore, 1983. https://computing.llnl.gov/sites/default/files/ODEPACK_pub1_u88007.pdf.

S. O. Fatunla, “Numerical integrators for stiff and highly oscillatory differential equations”, J. Math. Comput. 34 (1980) 373. https://www.jstor.org/stable/2006091.

O. B. Widlund, “A note on unconditionally stable Linear Multistep Methods”, BIT 7 (1967) 65. https://link.springer.com/article/10.1007/BF01934126#citeas.

P. Henrici, Discrete variable methods in ordinary differential equations, John Wiley, New York, 1962, pp. 407. https://www.amazon.com/Discrete-Variable-Ordinary-Differential-Equations/dp/0471372242.

Published

2025-02-01

How to Cite

A ninth-order first derivative method for numerical integration. (2025). Journal of the Nigerian Society of Physical Sciences, 7(1), 2028. https://doi.org/10.46481/jnsps.2025.2028

Issue

Volume 7, Issue 1, February 2025 (In Progress)

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2024 Richard O. Akinola, Ezekiel O. Omole, Joshua Sunday, Stephen Y. Kutchin

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

A ninth-order first derivative method for numerical integration. (2025). Journal of the Nigerian Society of Physical Sciences, 7(1), 2028. https://doi.org/10.46481/jnsps.2025.2028