Convolution equation and operators on the Euclidean motion group
Keywords:
Euclidean Motion group, invariant differential operator, Distribution, Universal enveloping algebraAbstract
Let $G = \mathbb{R}^2\rtimes SO(2)$ be the Euclidean motion group, let g be the Lie algebra of G and let U(g) be the universal enveloping algebra of g. Then U(g) is an infinite dimensional, linear associative and non-commutative algebra consisting of invariant differential operators on G. The Dirac measure on G is represented by $\delta_G$, while the convolution product of functions or measures on G is represented by $\ast$. Among other notable results, it is demonstrated that for each u in U(g), there is a distribution E on G such that the convolution equation $u\ast E = \delta_G$ is solved by method of convolution. Further more, it is established that the (convolution) operator $A^\prime : C^\infty_c(G)\rightarrow C^\infty(G),$, which is defined as $A^\prime f = f\ast T^n\delta(t)$ extends to a bounded linear operator on $L^2(G)$, for $f\in C^\infty_c(G)$, the space of infinitely differentiable functions on G with compact support. Furthermore, we demonstrate that the left convolution operator LT denoted as $L_Tf = T\ast f$ commutes with left translation, for $T\in D^\prime(G)$.
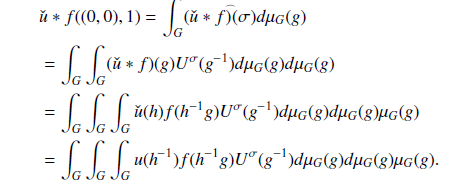
Published
How to Cite
Issue
Section
Copyright (c) 2024 U. N. Bassey, U. E. Edeke

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Similar Articles
- U. E. Edeke, U. N. Bassey, Some properties of convolution and spherical analysis on the Euclidean motion group , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 2, May 2025
- A. B. Disu, S. O. Salawu, Thermal distribution of magneto-tangent hyperbolic flowing fluid over a porous moving sheet: A Lie group analysis , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 1, February 2023
- Dyavappa B M, Velocity distribution of 43Ca+ion cloud in the low temperature limit in a quadrupole Penning Trap , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 1, February 2021
- B. M. Dyavappa, Energy distribution of an ion cloud in a quadrupole Penning Trap , Journal of the Nigerian Society of Physical Sciences: Volume 2, Issue 2, May 2020
- Pushap Lata Sharma, Mohini Kapalta, Ashok Kumar, Deepak Bains, Sumit Gupta, Pankaj Thakur, Electrohydro dynamics convection in dielectric rotating Oldroydian nanofluid in porous medium , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 2, May 2023
- Jamilu Adamu, B. M. Abdulhamid, D. T. Gbande, A. S. Halliru, Simple motion pursuit differential game problem of many players with integral and geometric constraints on controls function. , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 1, February 2021
- Adefemi Adeniran, A. A. Sodipo, C. G. Udomboso, A Modifed Forced Randomized Response Model , Journal of the Nigerian Society of Physical Sciences: Volume 2, Issue 1, February 2020
- Lamees K. Alzaki, Hassan Kamil Jassim, Time-Fractional Differential Equations with an Approximate Solution , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 3, August 2022
- B. J. Adekoya, B. O. Adebesin, V. U. Chukwuma, S. J. Adebiyi, S. O. Ikubanni, H. T. Oladunjoye, E. O. Adekoya, Pattern and variation of electron ionisation gradient as related to the plasma distribution mechanisms during the total solar eclipse of March 20, 2015 , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 2, May 2025
- Elsammani Ali Shokralla, Improving the thermal stability and dielectric properties of epoxy/phenolic resin type (novolac) composites by incorporating carbon nanofibers (CNFs) , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 1, February 2025
You may also start an advanced similarity search for this article.






