Shannon entropy and thermodynamic properties of an inversely quadratic Yukawa potential model

Authors

  • C. A. Onate Department of Physics, Bowen University, Iwo, Osun State, Nigeria
  • I. B. Okon Department of Physics, University of Uyo, Uyo, Nigeria
  • J. A. Akinpelu Department of Physics, Bowen University, Iwo, Osun State, Nigeria
  • O. O. Ajani Department of Physics, Bowen University, Iwo, Osun State, Nigeria
  • O. A. Adedewe Federal University of Technology, Akure, Ondo State, Nigeria
  • B. B. Deji-Jinadu Department of Physics, Bowen University, Iwo, Osun State, Nigeria

Keywords:

Bound states, EIgensolutions, Wave equation, Entropy, Thermal properties

Abstract

An inversely quadratic Yukawa potential is an exponential-type potential that has received little attention only in the bound state to the best of our understanding. This study obtained the solution of the Schrödinger equation for an inversely quadratic Yukawa potential via parametric Nikiforov-Uvarov method and supersymmetric approach. Some thermodynamic properties (vibrational enthalpy, vibrational Gibbs free energy and vibrational entropy) for the Inversely quadratic Yukawa potential are examined. The study is also applied to shannon entropy as the theoretic quantity. The results obtained showed that the energy eigenvalue for the potential goes in the opposite direction with the quantum state and the screening parameter. The Shannon entropy obtained as a function of the potential strength only obeyed the Heinsenberg principle at the ground state and excited states. In both cases, the also satisfied Bialynick-Birula, Mycielski inequality. It is noted that the thermal properties studied as a function of the temperature, even though the studied potential is not a molecular potential, the results followed the trend of the molecular potential.

Dimensions

M. Hamzavi, S. M. Ikhdair & B. I. Ita, “Approximate spin and pseudospin solutions to the Dirac equation for the inversely quadratic Yukawa potential and tensor interaction”, Physica Scripta 85 (2012) 045009. https://doi.org/10.1088/0031-8949/85/04/045009.

C. A. Onate, “Relativistic and Non-relativistic Solutions of the Inversely Quadratic Yukawa Potential”, African Review of Physics 8 (2013) 325.

A. Orlowski, “Information entropy and squeezing of quantum fluctuations ”, Physical Review A 56 (1997) 2545. https://doi.org/10.1103/PhysRevA.56.2545.

E. Omugbe, O. E. Osafile, I. J. Njoku, A. Jahanshir, C. O. Edet, I. B. Okon, E. S. Eyube, C. A. Onate, R. Horchani, E. S. William & A. N. Ikot, “Information-theoretic measures and thermodynamic properties under magnetic and Aharonov-Bohm flux fields ”, European Physical Journal D 77 (2023) 143. https://doi.org/10.1140/epjd/s10053-023-00718-1.

M. C. Onyeaju, E. Omugbe, C. A. Onate, I. B. Okon, E. S Eyube, U. S. Okorie, A. N. Ikot, D. A. Ogwu & O. P. Osuhor, “Information Theory and thermodynamic properties of diatomic molecules using Molecular potential”, Journal of Molecular Modeling 29 (2023) 311. https://doi.org/10.1007/s00894-023-05708-z

C. A. Onate, I. B. Okon, U. E. Vincent, E. Omugbe, E. S. Eyube, M. C. Onyeaju & G. O. Jude, “ Theoretic measure and thermal properties of a standard Morse potential model ”, Journal of Molecular Modeling 29 (2023) 34. https://doi.org/10.1007/s00894-022-05441-z.

J. S. Dehesa, I. V. Toranzo & D. Puertas-Centeno, “Entropic measures of Rydberg-like harmonic states ”, International Journal of Quantum Chemistry 117 (2017) 48. https://doi.org/10.1002/qua.25315.

W. A. Yahya, K. J. Oyewumi & K. D. Sen, “Quantum information entropies for the state Pöschl Teller-type potential ”, Journal of Mathematical Chemistry 54 (2016) 1810. https://doi.org/10.1007/s10910-016-0650-7.

S. A. Najafizade, H. Hassanabadi & S. Zarrinkamar, “Nonrelativistic Shannon information entropy for Kratzer potential”, Chinese Physics B 25 (2016) 040301. https://doi.org/10.1088/1674-1056/25/4/040301.

J. S. Dehesa, W. W. Assche & R. J. Yanez, “Information entropy of classical orthogonal polynomials and their application to the harmonic oscillator and Coulomb potentials”, Methods and Applications of Analysis 4 (1997) 91. https://dx.doi.org/10.4310/MAA.1997.v4.n1.a7.

C. Tezcan & R. Sever, “A General Approach for the exact Solution of the Schrödinger equation ”, International Journal of Theoretical Physics 48(2009) 337. https://doi.org/10.1007/s10773-008-9806-y.

C. A. Onate, M. O. Oluwayemi & I. B. Okon, “Dirac Equation for Energy-Dependent Potential with Energy-dependent Tensor Interaction”, Journal of the Nigerian Society of Physical Sciences 5 (2023) 917. https://doi.org/10.46481/jnsps.2023.917.

O. Bayrak, I. Boztosun & H. Ciftci, “Exact Analytical Solutions to the Kratzer Potential by the asymptotic iteration method”, International Journal of Quantum Chemistry 107 (2007) 540. https://doi.org/10.1002/qua.21141.

X. Y. Gu, S. H. Dong & Z. Q. Ma, “Energy spectra for modified Rosen-Morse potential solved by the exact quantization rule”, Journal of Physics A Mathematics and Theoretical (2009) 035303. https://doi.org/10.1088/1751-8113/42/3/035303.

W. C. Qiang & S. H. Dong, “Proper quantization rule”, EPL 89 (2010) 10003. https://doi.org/10.1209/0295-5075/89/10003.

S. H. Dong, R. Lemus & A. Frank, “Ladder operators for the Morse potential ”, International Journal of Quantum Chemistry 86 (2002) 433. https://doi.org/10.1002/qua.10038.

S. H. Dong, “The SU (2) realization for the Morse potential and its coherent states”, Canadian Journal of Physics 80 (2002) 129. https://doi.org/10.1139/p01-130.

G. H. Liu, Q. C. Ding, C. W. Wang & C. S. Jia, “ Unified explicit formulations of thermodynamic properties for the gas N O2 , and gaseous BF2 and AlCl2 radicals ”, Chem. Phys. Lett. 830 (2023) 140788. https://doi.org/10.1016/j.cplett.2023.140788. .

G. H. Liu, Q. C. Ding, C. W. Wang & C. S. Jia, “Unified non-fitting explicit formulation of thermodynamic properties for five compounds”, Journal of Molecular Structure 1294 (2023) 136543. https://doi.org/10.1016/j.molstruc.2023.136543.

Q. C. Ding, C. W. Wang, X. L. Peng, Y. Y. Lu, G. H. Liu, G. Li, L.S. Wei, J.Q. Chen. H. Yuan & C. S. Jia, “Unified analytical formulation regarding thermodynamic properties subject to gaseous metal hydroxides”, Journal of Molecular Structure 1298 (2024) 137075. https://doi.org/10.1016/j.molstruc.2023.137075.

C. W. Wang, X. L. Peng, J. Y. Liu, R. Jiang, X. P. Li, Y. S. Liu, S. Y. Liu, L. S. Wei, L. H. Zhang & C. S. Jia, “A novel formulation representation of the equilibrium constant for water gas shift reaction ”, International Journal of Hydrogen Energy 47 (2022) 27821. https://doi.org/10.1016/j.ijhydene.2022.06.105.

C. W. Wang, J. Li, L. H. Zhang, Q. C. Ding, G.H Liu, G. Li, R. Jiang, X. L. Peng, L. S. Wei, H. M. Tang, J. Y. Liu & C. S. Jia, “Non-fitting functional representation for the equilibrium constant subject to reaction between H2 S and CO2 ”, Fuel 362 (2024) 130916. https://doi.org/10.1016/j.fuel.2024.130918.

S. H. Dong & M. CruZ. Irisson, “Energy spectrum for a modified Rosen-Morse potential solved by proper quantization rule and its thermodynamic properties ”, Journal of Mathematical Chemistry 50 (2012) 881. https://doi.org/10.1007/s10910-011-9931-3.

S. H. Dong, M. Lozada-Cassou, J. Yu, F. Jimenze-Angeles & A. L. Rivera, “Hidden symmetries and thermodynamic properties for a harmonic oscillator plus an inverse square potential”, International Journal of Quantum Chemistry 107 (2007) 366. https://doi.org/10.1002/qua.21103.

M. Buchowiecki,“ Ro-vibrational coupling in high temperature thermochemistry of the BBr Molecule”, Chem. Phys. Lett. 692 (2018) 236 https://doi.org/10.1016/j.cplett.2017.12.051.

C. A. Onate, I. B. Okon, E. Omugbe, E. S. Eyube, B. A. AL-Asbahi, Y. A. Kumar, K. O. Emeje, E. Aghemenloh, A. R. Obasuyi, V. O. Obaje & T. O. Etchie. “Theoretical prediction of molar entropy of modified shifted Morse potential for gaseous molecules”, Chem. Phys. 582 (2024) 112294. https://doi.org/10.1016/j.chemphys.2024.112294.

Q. C. Ding, C. W. Wang, X. L. Peng, Y. Y. Lu, G. H. Liu, G. Li, L. S. Wei, J.Q. Chen, H. Yuan & C. S. Jia, “Unified analytical formulation regarding thermodynamic properties subject to gaseous metal hydroxides”, J. Mol. Struct. 1298 (2024) 137075. https://doi.org/10.1016/j.molstruc.2023.137075.

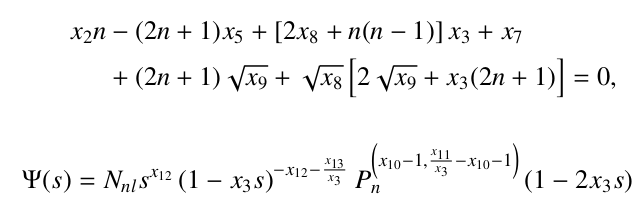
Published

2024-08-20

How to Cite

Shannon entropy and thermodynamic properties of an inversely quadratic Yukawa potential model. (2024). Journal of the Nigerian Society of Physical Sciences, 6(4), 2134. https://doi.org/10.46481/jnsps.2024.2134

Issue

Volume 6, Issue 4, November 2024

Section

Physics & Astronomy
Copyright & Licensing

Copyright (c) 2024 C. A. Onate, I. B. Okon, J. A. Akinpelu, O. O. Ajani, O. A. Adedewe, B. B. Deji-Jinadu

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Shannon entropy and thermodynamic properties of an inversely quadratic Yukawa potential model. (2024). Journal of the Nigerian Society of Physical Sciences, 6(4), 2134. https://doi.org/10.46481/jnsps.2024.2134