A numerical algorithm based on extended cubic B-spline functions for solving time-fractional convection-diffusion-reaction equation with variable coefficients

Authors

Keywords:

Time fractional convection-diffusion-reaction equation, Extended cubic B-spline basis functions, Caputo fractional derivative, Stability and convergence, Crank–Nicolson finite difference formulation

Abstract

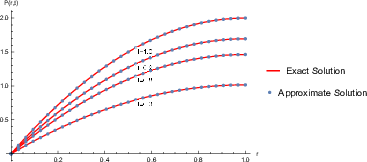
In this research, we develop an innovative and efficient numerical method for solving a nonlinear one-dimensional time-fractional convection-diffusion-reaction equation (TFCDRE) with a variable coefficient. This method integrates the Crank-Nicolson finite difference scheme with extended cubic B-spline (ExCBS) basis functions. The Caputo fractional derivative is applied for temporal discretization, while the ExCBS functions are utilized for spatial discretization. The stability of the method was discussed by the von Neumann method, which shows unconditional stability; and the convergence analysis secure an order of $O(h^2+\triangle t^{2-\alpha})$. We demonstrated the efficiency and simplicity of our method through three numerical experiments and verified its accuracy using the absolute error $(L_2)$ and maximum error $(L_\infty)$ norms in temporal and spatial dimensions. The results are also graphically represented and show substantial agreement with the approximated and exact solution. We confirmed the effectiveness and accuracy of our approach over the local discontinuous Galerkin finite element and the compact finite difference methods, respectively, from the literature.

Dimensions

R. Hilfer, Applications of fractional calculus in physics, World Scientific Publishing Co. Pte, Singapore, 2000. https://cir.nii.ac.jp/crid/1361137044225841024.

A. Ahmadova & N. I. Mahmudov, “Langevin differential equations with general fractional orders and their applications to electric circuit theory”, Journal of Computational and Applied Mathematics 388 (2021) 113299. https://doi.org/10.1016/j.cam.2020.113299.

R. O. Awonusika & O. A. Mogbojuri, “Approximate analytical solution of fractional lane-emden equation by mittag-leffler function method”, Journal of the Nigerian Society of Physical Sciences 4 (2022) 265. https://doi.org/10.46481/jnsps.2022.687.

K. A. Abro, A. Siyal, A. Atangana & Q. M. Al-Mdallal, “Analytical solution for the dynamics and optimization of fractional Klein–Gordon equation: an application to quantum particle”, Optical and Quantum Electronics 55 (2023) 704. https://doi.org/10.1007/s11082-023-04919-1.

A. A. Kilbas, H. M. Srivastava & J. J. Trulillo, Theory and applications of fractional differential equations, J. van Mill, Ed. Amsterdam: Elsevier, 2006. https://digital.library.tu.ac.th/tudc/frontend/Info/item/dc:17558.

K. M. Owolabi, A. Atangana & A. Akgul, “Modelling and analysis of fractal-fractional partial differential equations: application to reaction diffusion model”, Alexandria Engineering Journal 5 (2020) 2477. https://doi.org/10.1016/j.aej.2020.03.022.

A. O. Yunus & M. O. Olayiwola, “The analysis of a novel COVID19 model with the fractional-order incorporating the impact of the vaccination campaign in Nigeria via the Laplace-Adomian Decomposition Method”, Journal of the Nigerian Society of Physical Sciences (2024) 1830. https://doi.org/10.46481/jnsps.2024.1830.

J. Rashidinia, A. Momeni & M. Molavi-Arabshahi, “Solution of convection-diffusion model in groundwater pollution”, Scientific Reports 14 (2024) 2075. https://doi.org/10.1038/s41598-024-52393-w.

G. S. Teodoro, J. T. Machado & E. C. De Oliveira, “A review of definitions of fractional derivatives and other operators”, Journal of Computational Physics 388 (2019) 195. https://doi.org/10.1016/j.jcp.2019.03.008.

A. S. Hendy & M. A. Zaky, “A priori estimates to solutions of the time fractional convection–diffusion–reaction equation coupled with the Darcy system”, Communications in Nonlinear Science and Numerical Simulation 109 (2022) 106288. https://doi.org/10.1016/j.cnsns.2022.106288.

P. Prakash, K. Priyendhu & K. Anjitha, “Initial value problem for the (2+ 1)-dimensional time-fractional generalized convection–reaction– diffusion wave equation: invariant subspaces and exact solutions”, Computational and Applied Mathematics 41 (2022) 30. https://doi.org/10.1007/s40314-021-01721-1.

E. F. Anley, M. Basha, A. Hussain & B. Dai, “Numerical simulation for nonlinear space-fractional reaction convection-diffusion equation with its application”, Alexandria Engineering Journal 65 (2023) 245. https://doi.org/10.1016/j.aej.2022.10.047.

V. R. Hosseini, A. A. Mehrizi, H. Karimi-Maleh & M. Naddafi, “A numerical solution of fractional reaction–convection–diffusion for modeling PEM fuel cells based on a meshless approach”, Engineering Analysis with Boundary Elements 155 (2023) 707. https://doi.org/10.1016/j.enganabound.2023.06.016.

Y.-M. Wang & L. Ren, “Efficient compact finite difference methods for a class of time-fractional convection–reaction–diffusion equations with variable coefficients”, International Journal of Computer Mathematics, 96 (2019) 264. https://doi.org/10.1155/2019/7969371.

C.-S. Liu & C.-W. Chang, “Collocation method with fractional powers exponential trial functions for singularly perturbed reaction convection diffusion equation”, International Journal of Thermal Sciences 146 (2019) 106070. https://doi.org/10.1016/j.ijthermalsci.2019.106070.

C. Li & Z. Wang, “Numerical methods for the time fractional convection-diffusion-reaction equation”, Numerical Functional Analysis and Optimization 42 (2021) 1115. https://doi.org/10.1080/01630563.2021.1936019.

S¸ Toprakseven, “A weak Galerkin finite element method for time fractional reaction-diffusion-convection problems with variable coefficients”, Applied Numerical Mathematics 168 (2021) 1. https://doi.org/10.1016/j.apnum.2021.05.021.

E. Ngondiep, “A two-level fourth-order approach for timefractional convection–diffusion–reaction equation with variable coefficients”, Communications in Nonlinear Science and Numerical Simulation 111

(2022)106444. https://doi.org/10.1016/j.cnsns.2022.106444.

R. Choudhary, S. Singh & D. Kumar, “A second-order numerical scheme for the time-fractional partial differential equations with a time delay”, Computational and Applied Mathematics 41 (2022) 114. https://doi.org/10.1007/s40314-022-01810-9.

M. Naeem, N. H. Aljahdaly, R. Shah & W. Weera, “The study of fractional-order convection-reaction-diffusion equation via an Elzake Atangana-Baleanu operator”, AIMS Math 7 (2022) 18. https://doi.org/10.3934/math.2022995.

H. Yasmin, “Application of Aboodh homotopy perturbation transform method for fractional-order convection–reaction–diffusion equation within caputo and atangana–baleanu operators”, Symmetry bf15 (2023) 453. https://doi.org/10.3390/sym15020453.

Y. Zhang & M. Feng, “The virtual element method for the time fractional convection diffusion reaction equation with non-smooth data”, Computers & Mathematics with Applications 110 (2022) 1. https://doi.org/10.1016/j.camwa.2022.01.033.

F. M. Salama, N. Hj. Mohd. Ali & N. N. Abd Hamid, “Efficient hybrid group iterative methods in the solution of two-dimensional time fractional cable equation”, Advances in Difference Equations 2020 (2020) 257. https://doi.org/10.1186/s13662-020-02717-7.

F. M. Salama, N. N. Abd Hamid, N. H. M. Ali & U. Ali, “An efficient modified hybrid explicit group iterative method for the time-fractional diffusion equation in two space dimensions”, AIMS Mathematics bf7 (2022) 2370. https://doi.org/10.3934/math.2022134.

M. Basim, N. Senu, A. Ahmadian, Z. Ibrahim, and S. Salahshour, “Solving fractional variable-order differential equations of the non-singular derivative using Jacobi operational matrix”, Journal of the Nigerian Society of Physical Sciences 2 (2023) 1221. https://www.journal.nsps.org.ng/index.php/jnsps/article/view/1221.

L. Yan, S. Kumbinarasaiah, G. Manohara, H. M. Baskonus, and C. Cattani, “Numerical solution of fractional PDEs through wavelet approach”, Zeitschrift f¨ur angewandte Mathematik und Physik 75 (2024) 61. https://link.springer.com/article/10.1007/s00033-024-02195-x.

K. Issa, R. A. Bello, and U. J. Abubakar, “Approximate analytical solution of fractional-order generalized integro-differential equations via fractional derivative of shifted Vieta-Lucas polynomial”, Journal of the Nigerian Society of Physical Sciences (2024) 1821. https://doi.org/10.46481/jnsps.2024.1821.

H. Eltayeb, “Application of double Sumudu-generalized Laplace decomposition method and two-dimensional time-fractional coupled Burger’s equation”, Boundary Value Problems 2024 (2024) 48. https://doi.org/10.1186/s13661-024-01851-5.

R. Pant, G. Arora, B. K. Singh, and H. Emadifar, “Numerical solution of two-dimensional fractional differential equations using Laplace transform with residual power series method”, Nonlinear Engineering, 13 (2024) 20220347. https://doi.org/10.1515/nleng-2022-0347.

M. Yaseen and M. Abbas, “An efficient computational technique based on cubic trigonometric B-splines for time fractional Burgers’ equation”, International Journal of Computer Mathematics 97 (2020) 725. https://doi.org/10.1080/00207160.2019.1612053.

M. Shafiq, M. Abbas, K. M. Abualnaja, M. Huntul, A. Majeed & T. Nazir, “An efficient technique based on cubic B-spline functions for solving time-fractional advection diffusion equation involving Atangana–Baleanu derivative”, Engineering with Computers, pp. 1–17, 2021. https://doi.org/10.1007/s00366-021-01490-9.

P. Roul, V. Rohil, G. Espinosa-Paredes, and K. Obaidurrahman, “An efficient numerical method for fractional neutron diffusion equation in the presence of different types of reactivities”, Annals of Nuclear Energy 152 (2021) 108038. https://www.sciencedirect.com/science/article/abs/pii/S0306454920307349.

A. A. Okeke, N. N. A. Hamid, and M. Abbas, “A numerical technique for solving time-fractional Navier-Stokes equation with Caputo’s derivative using cubic B-spline functions”, in AIP Conference Proceedings, vol. 3016, no. 1. AIP Publishing, 2024. https://doi.org/10.1063/5.0193362.

P. Roul and V. P. Goura, “A high-order B-spline collocation scheme for solving a nonhomogeneous time-fractional diffusion equation”, Mathematical Methods in the Applied Sciences 44 (2021) 546. https://doi.org/10.1002/mma.6760.

M. Abbas, A. Bibi, A. S. Alzaidi, T. Nazir, A. Majeed, and G. Akram, “Numerical solutions of third-order time-fractional differential equations using cubic B-Spline functions”, Fractal and Fractional 6 (2022) 528.

https://doi.org/10.3390/fractalfract6090528.

A. Umer, M. Abbas, M. Shafiq, F. A. Abdullah, M. De la Sen, and T. Abdeljawad, “Numerical solutions of atangana-baleanu time-fractional advection diffusion equation via an extended cubic b-spline technique”, Alexandria Engineering Journal bf74 (2023) 285. https://doi.org/10.1016/j.aej.2023.05.028.

A. R. Hadhoud, A. A. Rageh, and T. Radwan, “Computational solution of the time-fractional schr¨odinger equation by using trigonometric bspline collocation method”, Fractal and Fractional 6 (2022) 127. https://doi.org/10.3390/fractalfract6030127.

T. Akram, A. Iqbal, P. Kumam, and T. Sutthibutpong, “Investigation of the fractional coupled-Burgers model with the exponential kernel”, Ain Shams Engineering Journal 15 (2024) 102450. https://doi.org/10.1016/j.asej.2023.102450.

U. Ghafoor, M. Abbas, T. Akram, E. K. El-Shewy, M. A. Abdelrahman & N. F. Abdo, “An efficient cubic b-spline technique for solving the time fractional coupled viscous burgers equation”, Fractal and Fractional 8 (2024) 93. https://doi.org/10.3390/fractalfract8020093.

F. Mirzaee & S. Alipour, “Cubic B-spline approximation for linear stochastic integro-differential equation of fractional order”, Journal of Computational and Applied Mathematics 366 (2020) 112440. https://www.sciencedirect.com/science/article/pii/S0377042719304431.

B. Khan, M. Abbas, A. S. Alzaidi, F. A. Abdullah & M. B. Riaz, “Numerical solutions of advection diffusion equations involving Atangana–Baleanu time fractional derivative via cubic B-spline approximations”, Results in Physics 42 (2022) 105941. https://www.sciencedirect.com/science/article/pii/S2211379722005605.

S. U. Arifeen, S. Haq & F. Golkarmanesh, “Computational study of multiterm time-fractional differential equation using cubic B-spline finite element method”, Complexity 2022 (2022) 3160725. https://doi.org/10.1155/2022/3160725.

B. Cao, X. Wu, Y. Wang & Z. Zhu, “Modified hybrid B-spline estimation based on spatial regulator tensor network for burger equation with nonlinear fractional calculus”, Mathematics and Computers in Simulation 220 (2024) 253. https://www.sciencedirect.com/science/article/abs/pii/S0378475424000156.

S. K. Sahoo, P. O. Mohammed, H. M. Srivastava, A. Kashuri, N. Chorfi & D. Baleanu, “Computational analysis of time fractional diffusion wave equation via novel B-splines-based technique”, AIMS Mathematics 9 (2024) 751. https://discovery.researcher.life/article/computational-analysis-of-time-fractional-diffusion-wave-equation-via-novel-b-splines-based-technique/edf7fad13893370682cee557fa3a0915.

I. Podlubny, Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Elsevier, 1998.

https://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=63919.

J. R. Poulin, Calculating infinite series using Parseval’s identity, The University of Maine, 2020. https://digitalcommons.library.umaine.edu/etd/3196/.

H. Xuli, “An extension of the cubic uniform B-spline curve”, Journal of Computer Aided Design and Computer Graphics 15 (2003) 576.

Y. Lin & C. Xu, “Finite difference/spectral approximations for the time fractional diffusion equation”, Journal of computational physics 225 (2007) 1533. https://doi.org/10.1016/j.jcp.2007.02.001.

S. Daochun, G. Zhendong, L. Weiqun & Y. Chao, “The order of complex numbers”, arXiv preprint 9 (2010). https://doi.org/10.48550/arXiv.1003.4906.

M. K. Kadalbajoo & P. Arora, “B-spline collocation method for the singular-perturbation problem using artificial viscosity”, Computers & Mathematics with Applications 57 (2009) 650. https://doi.org/10.1016/j.camwa.2008.09.008.

C. de Boor, “On the convergence of odd-degree spline interpolation”, Journal of approximation theory 1 (1968) 452. https://core.ac.uk/download/pdf/82288008.pdf.

C. Hall, “On error bounds for spline interpolation”, Journal of approximation theory 1 (1968) 209. https://doi.org/10.1016/0021-9045(68)90025-7.

Comparison plot of exact and approximate solutions with N = 32, ? = 0.45, ?t = 0.01 for Example 1 at different time levels.

Published

2025-02-01

How to Cite

A numerical algorithm based on extended cubic B-spline functions for solving time-fractional convection-diffusion-reaction equation with variable coefficients. (2025). Journal of the Nigerian Society of Physical Sciences, 7(1), 2323. https://doi.org/10.46481/jnsps.2025.2323

Issue

Volume 7, Issue 1, February 2025 (In Progress)

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2024 Anthony Anya Okeke, Nur Nadiah Abd Hamid, Wen Eng Ong, Muhammad Abbas

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

A numerical algorithm based on extended cubic B-spline functions for solving time-fractional convection-diffusion-reaction equation with variable coefficients. (2025). Journal of the Nigerian Society of Physical Sciences, 7(1), 2323. https://doi.org/10.46481/jnsps.2025.2323