Semi-analytical and numerical simulation of a coinfection model of Malaria and Zika virus disease
Keywords:
Malaria , Zika virus , Approximate Solution, Homotopy perturbationAbstract
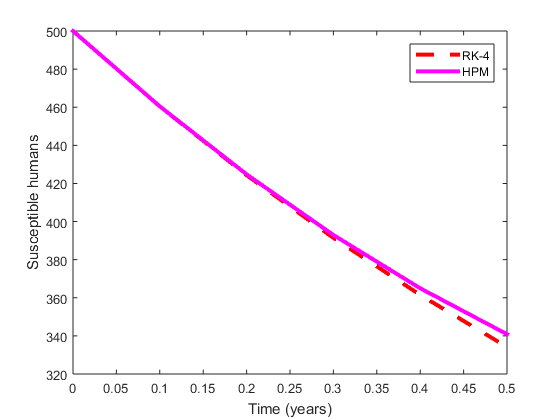
In this work, a model for the coinfection of malaria and zika virus disease is studied. The model incorporates various control measures against the spread of malaria and zika virus disease such as vaccination, treatment and biological control of mosquitoes using sterile insect technique. The existence and uniqueness of solutions to the model were first shown. Thereafter, the model is shown to be well-posed epidemiologically by showing that all solutions to the system are positive and bounded. Then, the solution of the model is obtained using the homotopy perturbation method which is a semi-analytical method. The solutions obtained are shown to be comparable with those obtained from Runge-Kutta method of order 4. Furthermore, the performance of the controls in comparison to each other when applied separately and when combined were shown. The results showed that combining the three controls performed better than the rest. Hence, efforts should be made to incorporate controls that affect both humans and the vectors for effective control of malaria, zika virus disease and their coinfection.
Published
How to Cite
Issue
Section
Copyright (c) 2025 E. C. Duru, M. C. Anyanwu , T. N. Nnamani , C. N. Nwosu, G. C. E. Mbah

This work is licensed under a Creative Commons Attribution 4.0 International License.







